DOI: https://doi.org/10.22201/fesc.20072236e.2021.12.23.1
COVID-19 epidemiological traffic light protocol in Mexico: an alternative classification using the FlowSort method
José Luis Romo Lozano
Profesor-Investigador de Tiempo Completo – Universidad Autónoma Chapingo
PDFResumen
El uso de protocolos de semáforo para la gestión de riesgos actualmente es ampliamente utilizado en todo el mundo por gobiernos, organizaciones no gubernamentales y empresas privadas. Un ejemplo de esto es la implementación de semáforos para administrar los riesgos de la pandemia COVID-19. El objetivo de esta investigación fue aplicar el método FlowSort como una alternativa distinta a la metodología actualmente usada por la Secretaría de Salud México. Se concluyó que es factible la utilización del método FlowSort, con la posibilidad de enriquecer la participación de los tomadores de decisiones mediante el uso de distintas funciones de preferencia.
Palabras clave: COVID-19, Clasificación, método FlowSort, semáforo
Abstract
Traffic light protocols for risk management are currently widely used throughout the world by governments, non-governmental organizations, and private companies. An example of this is the implementation of traffic lights to manage the risks of the COVID-19 pandemic. The objective of this research was to apply the FlowSort method as a different alternative to the methodology currently used by the Mexican Ministry of Health. It is concluded that the FlowSort method is feasible, with the possibility of enriching the participation of decision-makers through the use of different preference functions.
Keywords: COVID-19, Classification, FlowSort, traffic light
Introducción
Hoy en día la gestión de riesgos mediante protocolos de semáforo se utiliza ampliamente en todo el mundo por distintos tipos de organizaciones que incluyen: gobiernos, organizaciones no gubernamentales y empresas privadas (Kao et al., 2016). De igual modo, su aplicación abarca una gran variedad de actividades, ejemplo de estas son: riesgo clínico (Jones et al., 2021), salud mental (Juárez, 2020), sismicidad inducida por fracturación hidráulica (Shultz et al., 2020), estudios de la pobreza (Cavana, 2019), etiquetado nutricional (Ducrot et al., 2016) educación (Pinzón, Gómez & Romero, 2015), amenaza de erupción volcánica (De la Cruz-Reyna & Tilling, 2008) y, recientemente, en el tema del COVID-19 (Vizcaychipi et al., 2020). Generalmente, su uso tiene el objetivo de clasificar distintos niveles de una amenaza en particular para, en función de ello, diseñar respuestas que incluyen un conjunto de acciones específicas.
Derivado de la pandemia COVID-19 que actualmente padece el mundo, la inmensa mayoría de los países han implementado protocolos de semáforo para administrar los riesgos asociados. Algunos ejemplos son: los países miembros de la Unión Europea (European Centre for Disease Prevention & Control, 2021), Argentina (Rojo et al., 2020), Ecuador (Shakya et al., 2020) y México (Fajardo, 2020).
El semáforo epidemiológico que actualmente aplica la Secretaría de Salud de México consiste en cuatro colores (Secretaría de Salud, 2020): Verde (riesgo bajo), Amarillo (riesgo moderado), Naranja (riesgo alto) y Rojo (riesgo máximo) que se usan para definir un conjunto de medidas restrictivas, o permisivas, para gestionar los riesgos que se derivan de la pandemia. El grado de permisibilidad más alto corresponde al color verde y disminuye sucesivamente; esto es, Verde > Amarillo > Naranja > Rojo. Los colores se asignan a cada entidad federativa de acuerdo con las estadísticas reflejadas en un conjunto de indicadores.
La metodología reportada por la Secretaría de Salud de México para la asignación de los colores del semáforo utiliza 10 indicadores, de los cuales cuatro se expresan como tasas, tres como porcentajes y otros tres como tendencias.
- Tasa de reproducción efectiva (Rt) de COVID-19.
- Tasa de incidencia de casos estimados activos por 100 mil habitantes de los últimos 14 días (Ti).
- Tasa de mortalidad por 100 mil habitantes (Tm).
- Tasa de casos hospitalizados por 100 mil habitantes por 100 mil habitantes de los últimos 14 días (Th).
- Porcentaje de camas generales ocupadas en los hospitales dados de alta en la Red IRAG (PCg).
- Porcentaje de camas con ventilador ocupadas en los hospitales dados de alta en la Red IRAG (PCv).
- Porcentaje semanal de positividad al virus SARS-CoV-2 (PSp).
- Tendencia de presentación de casos de síndrome COVID-19 por 100 mil habitantes (TCs).
- Tendencia de la tasa de mortalidad por 100 mil habitantes de los últimos 14 días (TTm).
- Tendencia de personas hospitalizadas por IRAG en hospitales de la Red IRAG (TPh).
Una vez que se tienen los valores reportados y estimados de los distintos indicadores, cada uno de estos es convertido a una escala numérica del 0 al 4, de acuerdo con el rango de valores reflejados en estos, tal como se muestra en la tabla 1.
Tabla 1. Rangos y valores asignados a los indicadores en la escala 0-4
| Indicador | Rango | valor asignado | ||
|---|---|---|---|---|
| 1. Tasa de reproducción efectiva (Rt) de COVID-19 | ≥ 2.5 | 4 | ||
| 2.0 - 2.49 | 3 | |||
| 1.5 - 1.99 | 2 | |||
| 1 -1.49 | 1 | |||
| ≤ 0.99 | 0 | |||
| 2. Tasa de incidencia de casos estimados activos por 100 mil habitantes de los últimos 14 días (Ti) | ≥ 100 | 4 | ||
| 75 - 99.9 | 3 | |||
| 50 - 74.9 | 2 | |||
| 25 - 49.9 | 1 | |||
| ≤ 24.9 | 0 | |||
| 3. Tasa de mortalidad por cien mil habitantes (Tm) | ≥ 10 | 4 | ||
| 7.5 - 9.99 | 3 | |||
| 5.0 - 7.49 | 2 | |||
| 2.5 - 4.99 | 1 | |||
| ≤ 2.49 | 0 | |||
| 4. Tasa de casos hospitalizados por 100 mil habitantes por 100 mil habitantes (Th) | ≥40 | 4 | ||
| 30 – 39.9 | 3 | |||
| 20 – 29.9 | 2 | |||
| 11 -19.9 | 1 | |||
| ≤ 10.9 | 0 | |||
| 5. Porcentaje de ocupación camas generales IRAG (PCg) | ≥ 70 | 4 | ||
| 60 – 69.9 | 3 | |||
| 50 – 59.9 | 2 | |||
| 40 – 49.9 | 1 | |||
| ≤ 39.9 | 0 | |||
| 6. Porcentaje de ocupación camas con ventilador (PCv) | ≥ 70 | 4 | ||
| 60 – 69.9 | 3 | |||
| 50 – 59.9 | 2 | |||
| 40 – 49.9 | 1 | |||
| ≤ 39.9 | 0 | |||
| 7. Porcentaje de semanal de positividad al SARS-COV-2 (PSp) | ≥ 50 | 4 | ||
| 40 – 49.9 | 3 | |||
| 30 – 39.9 | 2 | |||
| 20 – 29.9 | 1 | |||
| ≤ 19.9 | 0 | |||
| 8. Tendencia de presentación de casos de síndrome COVID-19 (TCs) | ≥ 0.200 | 4 | ||
| 0.05 a 0.199 | 3 | |||
| -0.05 a 0.049 | 2 | |||
| -0.200 a – 0.049 | 1 | |||
| ≤ -0.21 | 0 | |||
| 9. Tendencia de mortalidad por cien mil habitantes (TTm) | ≥0.0200 | 4 | ||
| 0.005 a 0.0199 | 3 | |||
| -0.005 a 0.0049 | 2 | |||
| -0.0200 a – 0.0049 | 1 | |||
| ≤ -0.021 | 0 | |||
| 10. Tendencia personas hospitalizadas por cien mil habitantes (TPh) | ≥0.200 | 4 | ||
| 0.05 a 0.199 | 3 | |||
| -0.05 a 0.049 | 2 | |||
| -0.200 a – 0.049 | 1 | |||
| ≤ -0.21 | 0 |
Sobre la ponderación utilizada en los indicadores la información es incompleta. En la aplicación del semáforo se destacan dos etapas. La primera etapa ocurrió con la utilización de cinco indicadores, sus pesos de importancia se distribuían de la siguiente manera: PCg (30 %), PCv (¿%?), PPs (10 %), TPh (30 %) y TCs (30 %). Para la segunda etapa se agregaron otros cinco indicadores, pero no se reporta información sobre la redistribución de los pesos respectivos.
Finalmente, la clasificación de riesgo epidémico resulta de la sumatoria de los valores asignados a los distintos indicadores determinados con base en el rango en el que se ubican, como se muestra en la tabla 1. Adicionalmente, con base en precisiones y diálogos mantenidos con los gobiernos de las entidades, se hacen ajustes en los puntos finales y se determina el color del semáforo que se asigna a cada estado de la república.
El objetivo de la presente investigación fue utilizar la información proporcionada por la Secretaría de Salud (SS) del Gobierno Federal Mexicano para aplicar el método multicriterio FlowSort, como una alternativa distinta a la usada por la SS, para la clasificación de los estados de la república en los colores del semáforo epidemiológico COVID-19.
1. Materiales y métodos
La información de los criterios (indicadores) utilizada en este estudio, corresponde a la publicada el viernes 25 de septiembre de 2020 por la Secretearía de Salud, la cual se usó para determinar los colores asignados a cada estado, vigentes en el periodo 28 de septiembre – 11 de octubre de 2020 (tabla 2).
Tabla 2. Desempeño de los estados de la república en los distintos criterios, publicados el 25 de septiembre de 2020.
| Estado | Rt | Ti | Tm | Th | PCg % | PCv % | PSp % | TCs | TTm | TPh |
|---|---|---|---|---|---|---|---|---|---|---|
| Aguascalientes ($a_1$) | 0.93 | 19 | 4.3 | 9.19 | 22.61 | 40.2 | 27.4 | -0.7378836 | -0.022937864 | -0.1445319 |
| B. California ($a_2$) | 0.96 | 11.8 | 3.7 | 6.84 | 25.31 | 27.47 | 43.1 | -0.2181356 | 0.002960546 | -0.0932719 |
| B. California Sur ($a_3$) | 1.06 | 89.5 | 3.1 | 12.7 | 27.82 | 22.62 | 31 | 1.08696978 | -0.027675468 | -0.0873613 |
| Campeche ($a_4$) | 0.64 | 7.2 | 1.7 | 4.24 | 4.61 | 3.62 | 17.4 | -0.0544489 | -0.043058126 | -0.2168219 |
| Chiapas ($a_5$) | 1 | 1.1 | 0.1 | 0.59 | 5.91 | 4.56 | 20.5 | -0.0395808 | -0.001259624 | -0.0063801 |
| Chihuahua ($a_6$) | 0.69 | 14 | 1.6 | 5.55 | 21.79 | 24.37 | 48.2 | -0.1586209 | -0.009276188 | -0.0576669 |
| Cd. de México ($a_7$) | 0.96 | 68.5 | 4.6 | 23.94 | 43.75 | 41.42 | 27.7 | -0.4442578 | -0.015561405 | -0.0768346 |
| Coahuila ($a_8$) | 0.74 | 28.7 | 5.7 | 8.85 | 27.43 | 35.39 | 31.3 | -0.4363621 | -0.020834106 | -0.3164481 |
| Colima ($a_9$) | 0.67 | 39 | 7.3 | 14.73 | 51.52 | 31.78 | 59.2 | -0.2304296 | -0.052336965 | -0.2412446 |
| Durango ($a_{10}$) | 1.1 | 30.8 | 2.2 | 6.59 | 30.46 | 25.51 | 38.9 | -0.2474263 | -0.005448674 | -0.1900953 |
| E. de México ($a_{11}$) | 0.94 | 18.4 | 2.5 | 6.52 | 35.51 | 28.76 | 36.5 | -0.166671 | -0.001176787 | -0.0490668 |
| Guanajuato ($a_{12}$) | 0.96 | 38.7 | 2.3 | 5.22 | 22.85 | 8.98 | 40.5 | -0.187112 | -0.008712904 | -0.1398614 |
| Guerrero ($a_{13}$) | 1.26 | 27.6 | 1.9 | 5.36 | 36.79 | 15.73 | 58.2 | 0.04179949 | -0.01198285 | 0.08985987 |
| Hidalgo ($a_{14}$) | 0.8 | 17.9 | 4.1 | 8.53 | 36.83 | 18.02 | 54.4 | -0.123473 | -0.005901818 | -0.108764 |
| Jalisco ($a_{15}$) | 0.98 | 19.2 | 3.9 | 7.64 | 21.3 | 21.39 | 50.4 | -0.1566443 | 0.001439996 | -0.07377812 |
| Michoacán ($a_{16}$) | 0.96 | 23.4 | 3.1 | 6.81 | 35.06 | 24.72 | 47.6 | -0.0697948 | -0.012847524 | 0.0498594 |
| Morelos ($a_{17}$) | 0.81 | 7.7 | 1.2 | 4.96 | 21.27 | 13.92 | 32.5 | -0.1193039 | -0.013815215 | -0.04293254 |
| Nayarit ($a_{18}$) | 0.81 | 20.6 | 4.3 | 8.28 | 53.72 | 14.48 | 63.1 | -0.0989438 | -0.011328736 | -0.0209038 |
| Nuevo León ($a_{19}$) | 0.93 | 46.4 | 5.1 | 17.73 | 46.86 | 38.84 | 49.4 | -0.3303689 | -0.016543705 | -0.3800761 |
| Oaxaca ($a_{20}$) | 1.01 | 15.7 | 1.4 | 3.34 | 24.75 | 22.67 | 72.5 | -0.0255884 | -0.005026884 | 0.0040646 |
| Puebla ($a_{21}$) | 0.83 | 12.9 | 2.4 | 5.6 | 30.48 | 19.21 | 34.4 | -0.1085223 | -0.018249291 | -0.0847535 |
| Querétaro ($a_{22}$) | 0.99 | 19.3 | 4.7 | 8.12 | 23.13 | 27.21 | 54.9 | -0.2598809 | -0.02501685 | -0.1714441 |
| Quintana Roo ($a_{23}$) | 0.81 | 19.1 | 4.6 | 8.34 | 22.35 | 23.35 | 45.5 | -0.21102848 | -0.003843903 | -0.0435285 |
| San Luis Potosí ($a_{24}$) | 0.84 | 29.2 | 4.5 | 11.6 | 22.97 | 24.07 | 37.3 | -0.0998267 | -0.015793225 | 0.03624858 |
| Sinaloa ($a_{25}$) | 0.91 | 14.3 | 3.5 | 9.8 | 26.17 | 20.62 | 48.8 | -0.2180448 | -0.019071952 | -0.1089947 |
| Sonora ($a_{26}$) | 0.93 | 18.6 | 1.2 | 4.04 | 16.96 | 10.94 | 32.5 | -0.2281091 | -0.023295292 | 0.02241898 |
| Tabasco ($a_{27}$) | 0.83 | 32.3 | 2.3 | 6.76 | 23.09 | 17.37 | 31.6 | -0.229321 | -0.010112001 | -0.0548443 |
| Tamaulipas ($a_{28}$) | 0.97 | 22.3 | 2.4 | 10.06 | 24.8 | 15.81 | 36.8 | -0.1622378 | -0.023429086 | -0.2534232 |
| Tlaxcala ($a_{29}$) | 0.8 | 9 | 2 | 4.39 | 16.42 | 17.65 | 28.4 | -0.2847353 | -0.004020489 | 0.02024348 |
| Veracruz ($a_{30}$) | 0.94 | 13.3 | 1.9 | 6.15 | 33.96 | 21.65 | 53.5 | -0.0740543 | -0.003602682 | -0.070627 |
| Yucatán ($a_{31}$) | 0.9 | 40.9 | 2.8 | 11.52 | 19.85 | 15.11 | 43.2 | -0.0114609 | -0.001102987 | -0.3288958 |
| Zacatecas ($a_{32}$) | 0.99 | 30.7 | 4.7 | 6.97 | 26.85 | 28.93 | 48.4 | -0.198517 | 0.000973388 | -0.0847093 |
El método FlowSort
FlowSort (Nemery & Lamboray, 2008), es un método de clasificación multicriterio basado en la metodología PROMETHEE (Preference Ranking Organization Method for Enriched Evaluation), (Brans & Vincke, 1985), que asigna alternativas en categorías predefinidas y completamente ordenadas (Pelissari et al., 2019). Su utilización incluye una amplia cantidad de importantes actividades tales como: la evaluación de agilidad de respuesta por parte de hospitales en manejo de desastres (Moheimani et al., 2021); evaluación de capacidades de innovación y exportación de pequeñas y medianas empresas (Enjolras, Camargo & Schmitt, 2020); la asignación de alternativas en clusters individuales o de intervalo (Sarrazin, De Smet & Rosenfeld, 2018); la priorización de los factores causantes de fallas en la planificación de recursos empresariales (Rahmanimanesh et al., 2017) y la evaluación de cadenas de suministro (Sepúlveda & Derpich, 2014). Hasta ahora, no se sabe que en la literatura del tema se reporten aplicaciones del método en la clasificación de colores en protocolos de semáforo.
La utilización del método FlowSort hace uso de los siguientes componentes:
Un conjunto de alternativas a categorizar $𝐴=\{a_1 , a_2 , . . . , a_n \}$.
Un conjunto de criterios de desempeño de las alternativas $F=\{f_1, f_2 , . . . , f_m\}$.
Un grupo de perfiles de referencia $R=\{r_1 , . . . , r_{k+1} \}$, utilizados para definir cada categoría, donde $\dot{R}_i=R\cup \{a_i\}$ es el conjunto extendido de los perfiles, considerando cada alternativa $a_i$.
Un grupo de funciones de preferencia (Brans y Vincke, 1985), de las cuales se seleccionan aquellas que satisfagan las preferencias del tomador de decisiones.
Un conjunto K de categorías predefinidas $C_1 ,C_2, . . . , C_K$ , donde la categoría $C_1$ es la mejor y la categoría $C_K$ es la peor. Cada categoría es predefinida mediante perfiles límite o perfiles centrales. En el primer caso, cada categoría se define a partir de un límite superior $(r_j)$ y un límite inferior $(r_{j+1})$. En el segundo caso, las categorías se definen por un elemento central o centroide $(r_j^*)$.
Un conjunto de pesos asociados a cada criterio, $W=\{w_1,\ldots,w_m\}$, donde $\sum_{m=1}^{q} w_m=1$.
El método FlowSort, utiliza las metodologías PROMETHEE. Esto es, mediante la relación de superación (outranking) se contabilizan las preferencias entre cada una de las alternativas con el conjunto de perfiles definidos mediante comparaciones pareadas. Con base en esas comparaciones se estiman los flujos positivos $\left(\phi_{\dot{R}_j}^{+}\right)$, negativos $\left(\phi_{\dot{R}_j}^{-}\right)$ , y netos $\left(\phi_{\dot{R}_j}\right)$para cada alternativa, x en $\dot{R}$, mediante las ecuaciones (1), (2), y (3).
\begin{equation}
\phi_{\dot{R}_i}^{+}=\frac{1}{\lvert\dot{R}_l\rvert-1}\sum_{y\in\dot{R}_i} \pi(a_i,a_j)
\end{equation}
\begin{equation}
\phi_{\dot{R}_i}^{-}=\frac{1}{\lvert\dot{R}_l\rvert-1}\sum_{y\in\dot{R}_i} \pi(a_j,a_i)
\end{equation}
\begin{equation}
\phi_{\dot{R}_i}=\phi_{\dot{R}_i}^{+} + \phi_{\dot{R}_i}^{-}
\end{equation}
\begin{equation}
C_{\phi^+}(a_i)=C_h,if\phi_{\dot{R}_i}^{+}(r_h)\geq\phi_{\dot{R}_i}^{+}(a_i)>\phi_{\dot{R}_i}^{+}(r_{h+1})
\end{equation}
\begin{equation}
C_{\phi^-}(a_i)=C_h,if\phi_{\dot{R}_i}^{-}(r_h)\geq\phi_{\dot{R}_i}^{-}(a_i)\leq\phi_{\dot{R}_i}^{-}(r_{h+1})
\end{equation}
Donde $\pi(a_i,a_j)$ es el grado de preferencia que expresa la preferencia global de la alternativa $a_i$ sobre $a_j$ de acuerdo con todos los criterios.
Posteriormente, se determina la asignación las clases a cada alternativa mediante las reglas de asignación (4) y (5). Cuando se presentan conflictos entre (4) y (5), se hace uso de los flujos netos (Sepulveda, 2014).
Otra manera de ver el método FlowSort es que este simplemente prioriza el conjunto $\dot{R}_i$ para cada $a_i$, y la identificación de la clase correspondiente se determina a partir de la posición $a_i$ de entre los perfiles $r_h$ y $r_{h+1}$(Ishizaka & Nemery, 2013).
En la aplicación del método FlowSort para la determinación de los colores del semáforo COVID-19, la información disponible se consideró de la siguiente manera:
- Las alternativas son los estados de la república $𝐴=\{a_1 , a_2 , \ldots, a_{32} \}$;
- Los criterios de desempeño son los indicadores $F=\{f_1 , f_2 , \ldots, f_{10} \}$;;
- La función de preferencia utilizada es la llamada usual (figura 1), donde la preferencia se define mediante las fórmulas en (6);
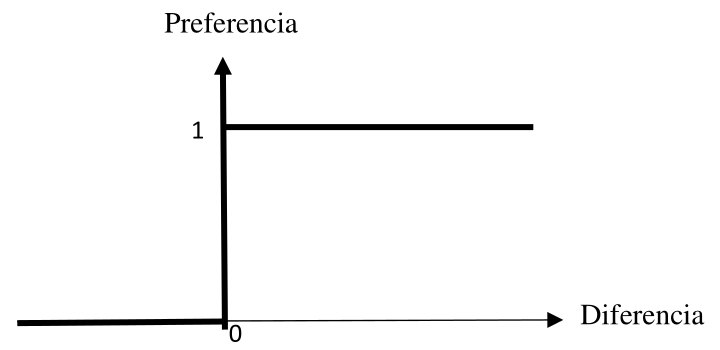
Figura 1. Función de preferencia usual (Brans and De Simet, 2016)
\begin{equation}
Preferencia=\left\{ \begin{array}{ll}
0 & \mbox{si $f_k(a_i)-f_k(a_j) \leq 0$,} \\
1 & \mbox{si $f_k(a_i)-f_k(a_j) > 0$,}
\end{array}
\right.
\end{equation}
- Las categorías, o clases, equivalen a los colores del semáforo COVID-19, {verde, amarillo, naranja, y rojo};
- Los perfiles límite que determinan los colores son $\{r_1, r_2,\ldots,r_4 \}$ (tabla 3), los cuales se basaron en los rangos especificados en el proceso de asignación de los valores de la escala 0-4 (tabla 1), Secretaría de Salud (2020).
Tabla 3. Perfiles que definen los distintos colores del semáforo
| Color\criterios | Rt | Ti | Tm | Th | PCg | PCv | PSp | TCs | TTm | TPh |
|---|---|---|---|---|---|---|---|---|---|---|
| Verde | ≤ 1.49 | ≤ 49.9 | ≤ 4.99 | ≤ 19.9 | ≤ 49.9 | ≤ 49.9 | ≤ 29.9 | ≤ -0.049 | ≤ -0.0049 | ≤ -0.049 |
| Amarillo | 1.99 | 74.9 | 7.49 | 29.9 | 59.9 | 59.9 | 39.9 | 0.049 | 0.0049 | 0.049 |
| Naranja | 2.49 | 99.9 | 9.99 | 39.9 | 69.9 | 69.9 | 49.9 | 0.199 | 0.0199 | 0.199 |
| Rojo | ≥ 2.5 | ≥ 100 | ≥10 | ≥ 40 | ≥ 70 | ≥ 70 | ≥50 | ≥0.200 | ≥ 0.0200 | ≥0.200 |
- Finalmente, para complementar la aplicación, los pesos de importancia $W=\{w_1,w_2,\ldots,w_{10}\}$, asignados a cada criterio fueron: Rt (0.10), Ti (0.15), Tm (0.10), Th (0,15), PCg (0.05), PCv (0.05), PSp (0.10), TCs (0.10), TTm (0.10), TPh (0.10). Estos se determinaron buscando un equilibrio con los que original y parcialmente se asignaron durante la primera etapa de la operación del semáforo. Asimismo, es relevante indicar que todos los criterios utilizados son a minimizar. Esto quiere decir que todos están orientados en la misma dirección (negativa), lo que implica que un valor grande de cualquiera de ellos contribuye a la asignación de un color menos permisivo; mientras que un valor pequeño contribuye en sentido contrario (Brüggeman & Patil, 2011).
Con la idea de observar las diferencias entre el método utilizado por la Secretaría de Salud y el método FlowSort, se presentan la tabla 4 y la figura 2.
Tabla 4. Comparación entre los procesos de clasificación de ambos métodos
| Método de la Secretaría de Salud | Método FlowSort |
Resultado
|
Resultado
|
Fuente: Elaboración propia
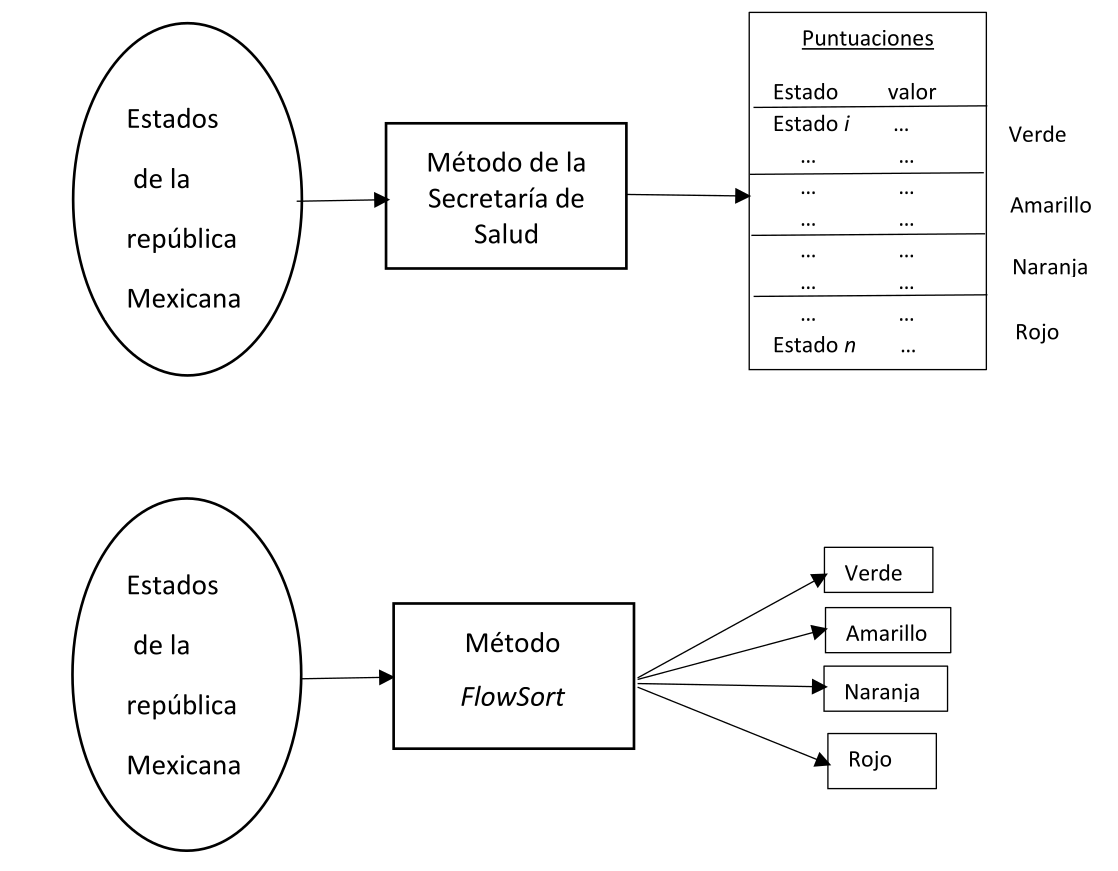
Figura 2. Comparación entre los métodos de clasificación aplicados en la asignación de colores del Semáforo COVID-19. (La parte inferior de la figura es una modificación de la presentada por Ishizaka y Nemery (2013).
2. Resultados y discusión
Del análisis de las condiciones que cada estado presenta en sus indicadores (tabla 2), sobresale que ninguno de ellos tiene la mejor de las condiciones en todos los indicadores, entendiendo como mejores condiciones aquellas donde se presenta el menor valor en los indicadores, ya que se deben minimizar. De este modo, el estado de Colima tiene el menor valor (0.67) en el indicador Tasa de reproducción efectiva de COVID-19 (Rt). Por su parte, el estado de Chiapas supera al resto de las entidades en los siguientes indicadores: Tasa de incidencia de casos estimados activos por 100 mil habitantes (Ti = 1.1); Tasa de mortalidad por 100 mil habitantes (Tm= 0.10); Tasa de casos hospitalizados por 100 mil habitantes (Th = 0.59); Porcentaje de camas generales ocupadas en la red IRAG (conjunto de unidades hospitalarias del Sistema Nacional de Salud) (PCg = 5.91); Porcentaje de camas con ventilador en hospitales de la red IRAG (PCv = 4.56), y Porcentaje semanal de positividad al virus SARS-CoV2 (PSp = 20.5). Sin embargo, este estado es superado por varias entidades en los indicadores Tendencia de presentación de casos de síndrome COVID-19 por 100 mil habitantes (TCs), Tendencia de la tasa de mortalidad por 100 mil habitantes (TTm) y Tendencia de personas hospitalizadas en hospitales de la red IRAG (TPh). Esta situación de no superación unánime es el caso típico de problemas multicriterio.
La utilización del método FlowSort en la clasificación de los estados se desarrolló mediante el software Smart Picker y dentro de este proceso se estimaron las preferencias globales de cada estado con respecto a cada perfil límite, $\pi(a_i,r_j)$ , así como las preferencias globales de los perfiles límite con respecto a cada estado, $\pi(r_j,a_i)$, (tabla 5). Estos valores nos sirven para identificar tres aspectos distintos que se presentan en el análisis de las relaciones de superación (outranking) entre los estados y el conjunto de perfiles límite y viceversa: indiferencia, preferencia e incomparabilidad (Ishizaka & Nemery, 2013). Cuando las preferencias son similares y con valores pequeños, < 0.5, $(\pi_{ij} \approx 0 \approx \pi_{ji})$, las alternativas comparadas se identifican como indiferentes. Cuando hay una diferencia alta entre las preferencias, $\lvert\pi_{ij}-\pi_{ji}\rvert\gg0$ , entonces la preferencia está completamente definida. La incomparabilidad se presenta cuando ambos valores son similares y grandes, $\pi_{ij} \approx 0.5 \approx \pi_{ji}$.
Con base en lo anterior, se puede afirmar que la mayoría de las relaciones de superación entre los estados y los perfiles límite se encuentran definidas y no se identifican indiferencias. Se pueden observar algunas incomparabilidades, tal es el caso de los estados de Chiapas ($a_5$), Estado de México ($a_{11}$), Hidalgo ($a_{14}$), Jalisco ($a_{15}$), y Michoacán ($a_{16}$) todos ellos con respecto al perfil límite $r_1$ (Cuadro 5).
Generalmente, las incomparabilidades son prácticamente inevitables en las relaciones binarias de superación (Lariechev, 2001) y una de las resultantes es que pueden producir órdenes de prioridades incompletos. En este caso ese problema se elimina mediante la consideración de los flujos netos, (fórmula 3).
Tabla 5. Preferencias globales entre estados y criterios límite.
| Preferencias | r1 | r2 | r3 | r4 |
|---|---|---|---|---|
| $ \pi(a_{1},r_j)$ | 0.65 | 1 | 1 | 1 |
| $ \pi(r_j,a_{1})$ | 0.35 | 0 | 0 | 0 |
| $ \pi(a_{2},r_j)$ | 0.6 | 0.8 | 0.9 | 1 |
| $ \pi(r_j,a_{2})$ | 0.4 | 0.2 | 0.1 | 0 |
| $ \pi(a_{3},r_j)$ | 0.2 | 0.65 | 0.75 | 0.9 |
| $ \pi(r_j,a_{3})$ | 0.8 | 0.35 | 0.25 | 0.1 |
| $ \pi(a_{4},r_j)$ | 0.9 | 1 | 1 | 1 |
| $ \pi(r_j,a_{4})$ | 0.1 | 0 | 0 | 0 |
| $ \pi(a_{5},r_j)$ | 0.5 | 0.7 | 1 | 1 |
| $ \pi(r_j,a_{5})$ | 0.5 | 0.3 | 0 | 0 |
| $ \pi(a_{6},r_j)$ | 0.6 | 0.9 | 0.9 | 1 |
| $ \pi(r_j,a_{6})$ | 0.4 | 0.1 | 0.1 | 0 |
| $ \pi(a_{7},r_j)$ | 0.2 | 0.7 | 1 | 1 |
| $ \pi(r_j,a_{7})$ | 0.8 | 0.3 | 0 | 0 |
| $ \pi(a_{8},r_j)$ | 0.55 | 0.8 | 1 | 1 |
| $ \pi(r_j,a_{8})$ | 0.45 | 0.2 | 0 | 0 |
| $ \pi(a_{9},r_j)$ | 0.45 | 0.75 | 0.9 | 0.9 |
| $ \pi(r_j,a_{9})$ | 0.55 | 0.25 | 0.1 | 0.1 |
| $ \pi(a_{10},r_j)$ | 0.45 | 0.9 | 1 | 1 |
| $ \pi(r_j,a_{10})$ | 0.55 | 0.1 | 0 | 0 |
| $ \pi(a_{11},r_j)$ | 0.5 | 0.8 | 1 | 1 |
| $ \pi(r_j,a_{11})$ | 0.5 | 0.2 | 0 | 0 |
| $ \pi(a_{12},r_j)$ | 0.45 | 0.9 | 0.9 | 1 |
| $ \pi(r_j,a_{12})$ | 0.55 | 0.1 | 0.1 | 0 |
| $ \pi(a_{13},r_j)$ | 0.35 | 0.7 | 0.8 | 0.9 |
| $ \pi(r_j,a_{13})$ | 0.65 | 0.3 | 0.2 | 0.1 |
| $ \pi(a_{14},r_j)$ | 0.5 | 0.9 | 0.9 | 0.9 |
| $ \pi(r_j,a_{14})$ | 0.5 | 0.1 | 0.1 | 0.1 |
| $ \pi(a_{15},r_j)$ | 0.5 | 0.8 | 0.9 | 0.9 |
| $ \pi(r_j,a_{15})$ | 0.5 | 0.2 | 0.1 | 0.1 |
| $ \pi(a_{16},r_j)$ | 0.5 | 0.8 | 0.8 | 1 |
| $ \pi(r_j,a_{16})$ | 0.5 | 0.2 | 0.2 | 0 |
| $ \pi(a_{17},r_j)$ | 0.6 | 0.8 | 1 | 1 |
| $ \pi(r_j,a_{17})$ | 0.4 | 0.2 | 0 | 0 |
| $ \pi(a_{18},r_j)$ | 0.45 | 0.75 | 0.9 | 0.9 |
| $ \pi(r_j,a_{18})$ | 0.55 | 0.25 | 0.1 | 0.1 |
| $ \pi(a_{19},r_j)$ | 0.35 | 0.8 | 0.9 | 1 |
| $ \pi(r_j,a_{19})$ | 0.65 | 0.2 | 0.1 | 0 |
| $ \pi(a_{20},r_j)$ | 0.6 | 0.7 | 0.9 | 0.9 |
| $ \pi(r_j,a_{20})$ | 0.4 | 0.3 | 0.1 | 0.1 |
| $ \pi(a_{21},r_j)$ | 0.6 | 0.9 | 1 | 1 |
| $ \pi(r_j,a_{21})$ | 0.4 | 0.1 | 0 | 0 |
| $ \pi(a_{22},r_j)$ | 0.7 | 0.9 | 0.9 | 0.9 |
| $ \pi(r_j,a_{22})$ | 0.3 | 0.1 | 0.1 | 0.1 |
| $ \pi(a_{23},r_j)$ | 0.6 | 0.7 | 0.9 | 1 |
| $ \pi(r_j,a_{23})$ | 0.4 | 0.3 | 0.1 | 0 |
| $ \pi(a_{24},r_j)$ | 0.2 | 0.8 | 1 | 1 |
| $ \pi(r_j,a_{24})$ | 0.8 | 0.2 | 0 | 0 |
| $ \pi(a_{25},r_j)$ | 0.6 | 0.9 | 0.9 | 1 |
| $ \pi(r_j,a_{25})$ | 0.4 | 0.1 | 0.1 | 0 |
| $ \pi(a_{26},r_j)$ | 0.8 | 0.8 | 1 | 1 |
| $ \pi(r_j,a_{26})$ | 0.1 | 0.2 | 0 | 0 |
| $ \pi(a_{27},r_j$ | 0.55 | 0.9 | 1 | 1 |
| $ \pi(r_j,a_{27})$ | 0.45 | 0.1 | 0 | 0 |
| $ \pi(a_{28},r_j)$ | 0.8 | 0.9 | 1 | 1 |
| $ \pi(r_j,a_{28})$ | 0.2 | 0.1 | 0 | 0 |
| $ \pi(a_{29},r_j)$ | 0.7 | 0.8 | 1 | 1 |
| $ \pi(r_j,a_{29})$ | 0.3 | 0.2 | 0 | 0 |
| $ \pi(a_{30},r_j)$ | 0.6 | 0.8 | 0.9 | 0.9 |
| $ \pi(r_j,a_{30})$ | 0.4 | 0.2 | 0.1 | 0.1 |
| $ \pi(a_{31},r_j)$ | 0.3 | 0.7 | 0.9 | 1 |
| $ \pi(r_j,a_{31})$ | 0.7 | 0.3 | 0.1 | 0 |
| $ \pi(a_{32},r_j)$ | 0.35 | 0.8 | 0.9 | 1 |
| $ \pi(r_j,a_{32})$ | 0.65 | 0.2 | 0.1 | 0 |
La tabla 6 presenta los flujos estimados para cada entidad de la República Mexicana para los datos del 25 de septiembre de 2020. El flujo neto $\Phi_{ai}$ constituye el índice de evaluación general del desempeño de las alternativas (estados). Las alternativas más preferidas son las que tienen los flujos netos más altos, mientras que las alternativas con los flujos netos más bajos se consideran las menos preferidas (Spronk et al., 2005). De este modo, observamos que hay 10 estados que representan los valores más grandes en sus flujos netos, todos ellos mayores a 0.7 y, por lo tanto, el método les asigna el color más permisivo, (Verde): Aguascalientes, Campeche, Chihuahua, Morelos, Puebla, Sinaloa, Sonora, Tabasco, Tamaulipas y Tlaxcala. De todos ellos, sobresale Campeche con un flujo neto de 0.95.
Una forma de visualizar la asignación de los colores es observar el valor del flujo neto del estado de interés. Los colores están delimitados por los flujos netos en los perfiles límite de la siguiente manera: a cualquier valor $\geq r_1$ , le corresponde el color verde; para valores menores que $r_1$ pero mayor o igual que $r_2$, se les asigna el color amarillo: para valores menores que $r_2$ y mayores o iguales a $r_3$, el color naranja y para valores menores que $r_3$ y mayores o iguales a $r_4$, el color rojo. Como ejemplo, veamos el caso de Baja California cuyo valor de su flujo neto es de 0.65, el cual se encuentra entre los valores de los perfiles límite $r_1$ (0.7) y $r_2$ (0.1). Estos perfiles delimitan el color amarillo, por lo cual a Baja California le corresponde dicho color.
Tabla 6. Flujos positivos, negativos y netos
| Estado | Conjunto ampliado | Flujos | r1 | r2 | r3 | r4 | Puntaje | Color asignado | Diferencia con SS |
|---|---|---|---|---|---|---|---|---|---|
| Aguascalientes | $\dot{R}_{a1}$ | $\Phi_{+ \atop {a1}}$ | 0.8375 | 0.5 | 0.25 | 0 | 0.9125 | ||
| $\Phi_{- \atop {a1}}$ | 0.1625 | 0.5 | 0.75 | 1 | 0.0875 | ||||
| $\Phi_{ \atop {a1}}$ | 0.675 | 0 | -0.5 | -1 | 0.825 | Verde | -1 | ||
| Baja California | $\dot{R}_{a2}$ | $\Phi_{+ \atop {a2}}$ | 0.85 | 0.55 | 0.275 | 0 | 0.825 | ||
| $\Phi_{- \atop {a2}}$ | 0.15 | 0.45 | 0.725 | 1 | 0.175 | ||||
| $\Phi_{ \atop {a2}}$ | 0.7 | 0.1 | -0.45 | -1 | 0.65 | Amarillo | -1 | ||
| Baja California Sur | $\dot{R}_{a3}$ | $\Phi_{+ \atop {a3}}$ | 0.95 | 0.5875 | 0.3125 | 0.025 | 0.625 | ||
| $\Phi_{- \atop {a3}}$ | 0.05 | 0.4125 | 0.6875 | 0.975 | 0.375 | ||||
| $\Phi_{ \atop {a3}}$ | 0.9 | 0.175 | -0.375 | -0.95 | 0.25 | Amarillo | -1 | ||
| Campeche | $\dot{R}_{a4}$ | $\Phi_{+ \atop {a4}}$ | 0.775 | 0.5 | 0.25 | 0 | 0.975 | ||
| $\Phi_{- \atop {a4}}$ | 0.225 | 0.5 | 0.75 | 1 | 0.025 | ||||
| $\Phi_{ \atop {a4}}$ | 0.55 | 0 | -0.5 | -1 | 0.95 | Verde | -1 | ||
| Chiapas | $\dot{R}_{a5}$ | $\Phi_{+ \atop {a5}}$ | 0.875 | 0.575 | 0.25 | 0 | 0.8 | ||
| $\Phi_{- \atop {a5}}$ | 0.125 | 0.425 | 0.75 | 1 | 0.2 | ||||
| $\Phi_{ \atop {a5}}$ | 0.75 | 0.15 | -0.5 | -1 | 0.6 | Amarillo | 0 | ||
| Chihuahua | $\dot{R}_{a6}$ | $\Phi_{+ \atop {a6}}$ | 0.85 | 0.525 | 0.275 | 0 | 0.85 | ||
| $\Phi_{- \atop {a6}}$ | 0.15 | 0.475 | 0.725 | 1 | 0.15 | ||||
| $\Phi_{ \atop {a6}}$ | 0.7 | 0.05 | -0.45 | -1 | 0.7 | Verde | -1 | ||
| Ciudad de México | $\dot{R}_{a7}$ | $\Phi_{+ \atop {a7}}$ | 0.95 | 0.575 | 0.25 | 0 | 0.725 | ||
| $\Phi_{- \atop {a7}}$ | 0.05 | 0.425 | 0.75 | 1 | 0.275 | ||||
| $\Phi_{ \atop {a7}}$ | 0.9 | 0.15 | -0.5 | -1 | 0.45 | Amarillo | -1 | ||
| Coahuila | $\dot{R}_{a8}$ | $\Phi_{+ \atop {a8}}$ | 0.8625 | 0.55 | 0.25 | 0 | 0.8375 | ||
| $\Phi_{- \atop {a8}}$ | 0.1375 | 0.45 | 0.75 | 1 | 0.1625 | ||||
| $\Phi_{ \atop {a8}}$ | 0.725 | 0.1 | -0.5 | -1 | 0.675 | Amarillo | 0 | ||
| Colima | $\dot{R}_{a9}$ | $\Phi_{+ \atop {a9}}$ | 0.8875 | 0.5625 | 0.275 | 0.025 | 0.75 | ||
| $\Phi_{- \atop {a9}}$ | 0.1125 | 0.4375 | 0.725 | 0.975 | 0.25 | ||||
| $\Phi_{ \atop {a9}}$ | 0.775 | 0.125 | -0.45 | -0.95 | 0.5 | Amarillo | -1 | ||
| Durango | $\dot{R}_{a10}$ | $\Phi_{+ \atop {a10}}$ | 0.8875 | 0.525 | 0.25 | 0 | 0.8375 | ||
| $\Phi_{- \atop {a10}}$ | 0.1125 | 0.475 | 0.75 | 1 | 0.1625 | ||||
| $\Phi_{ \atop {a10}}$ | 0.775 | 0.05 | -0.5 | -1 | 0.675 | Amarillo | 0 | ||
| Estado de México | $\dot{R}_{a11}$ | $\Phi_{+ \atop {a11}}$ | 0.875 | 0.55 | 0.25 | 0 | 0.825 | ||
| $\Phi_{- \atop {a11}}$ | 0.125 | 0.45 | 0.75 | 1 | 0.175 | ||||
| $\Phi_{ \atop {a11}}$ | 0.75 | 0.1 | -0.5 | -1 | 0.65 | Amarillo | -1 | ||
| Guanajuato | $\dot{R}_{a12}$ | $\Phi_{+ \atop {a12}}$ | 0.8875 | 0.525 | 0.275 | 0 | 0.8125 | ||
| $\Phi_{- \atop {a12}}$ | 0.1125 | 0.475 | 0.725 | 1 | 0.1875 | ||||
| $\Phi_{ \atop {a12}}$ | 0.775 | 0.05 | -0.45 | -1 | 0.625 | Amarillo | 0 | ||
| Guerrero | $\dot{R}_{a13}$ | $\Phi_{+ \atop {a13}}$ | 0.9125 | 0.575 | 0.3 | 0.025 | 0.6875 | ||
| $\Phi_{- \atop {a13}}$ | 0.0875 | 0.425 | 0.7 | 0.975 | 0.3125 | ||||
| $\Phi_{ \atop {a13}}$ | 0.825 | 0.15 | -0.4 | -0.95 | 0.375 | Amarillo | -1 | ||
| Hidalgo | $\dot{R}_{a14}$ | $\Phi_{+ \atop {a14}}$ | 0.875 | 0.525 | 0.275 | 0.025 | 0.8 | ||
| $\Phi_{- \atop {a14}}$ | 0.125 | 0.475 | 0.725 | 0.975 | 0.2 | ||||
| $\Phi_{ \atop {a14}}$ | 0.75 | 0.05 | -0.45 | -0.95 | 0.6 | Amarillo | -1 | ||
| Jalisco | $\dot{R}_{a15}$ | $\Phi_{+ \atop {a15}}$ | 0.875 | 0.55 | 0.275 | 0.025 | 0.775 | ||
| $\Phi_{- \atop {a15}}$ | 0.125 | 0.45 | 0.725 | 0.975 | 0.225 | ||||
| $\Phi_{ \atop {a15}}$ | 0.75 | 0.1 | -0.45 | -0.95 | 0.55 | Amarillo | -1 | ||
| Michoacán | $\dot{R}_{a16}$ | $\Phi_{+ \atop {a16}}$ | 0.875 | 0.55 | 0.3 | 0 | 0.775 | ||
| $\Phi_{- \atop {a16}}$ | 0.125 | 0.45 | 0.725 | 0.975 | 0.225 | ||||
| $\Phi_{ \atop {a16}}$ | 0.75 | 0.1 | -0.4 | -1 | 0.55 | Amarillo | -1 | ||
| Morelos | $\dot{R}_{a17}$ | $\Phi_{+ \atop {a17}}$ | 0.85 | 0.55 | 0.25 | 0 | 0.85 | ||
| $\Phi_{- \atop {a17}}$ | 0.125 | 0.45 | 0.725 | 0.975 | 0.225 | ||||
| $\Phi_{ \atop {a17}}$ | 0.7 | 0.1 | -0.5 | -1 | 0.7 | Verde | -1 | ||
| Nayarit | $\dot{R}_{a18}$ | $\Phi_{+ \atop {a18}}$ | 0.8875 | 0.5625 | 0.275 | 0.025 | 0.75 | ||
| $\Phi_{- \atop {a18}}$ | 0.1125 | 0.4375 | 0.725 | 0.975 | 0.25 | ||||
| $\Phi_{ \atop {a18}}$ | 0.775 | 0.125 | -0.45 | -0.95 | 0.5 | Amarillo | -1 | ||
| Nuevo León | $\dot{R}_{a19}$ | $\Phi_{+ \atop {a19}}$ | 0.9125 | 0.55 | 0.275 | 0 | 0.7625 | ||
| $\Phi_{- \atop {a19}}$ | 0.0875 | 0.45 | 0.725 | 1 | 0.2375 | ||||
| $\Phi_{ \atop {a19}}$ | 0.825 | 0.1 | -0.45 | -1 | 0.525 | Amarillo | -1 | ||
| Oaxaca | $\dot{R}_{a20}$ | $\Phi_{+ \atop {a20}}$ | 0.875 | 0.575 | 0.275 | 0.025 | 0.75 | ||
| $\Phi_{- \atop {a20}}$ | 0.125 | 0.425 | 0.725 | 0.975 | 0.25 | ||||
| $\Phi_{ \atop {a20}}$ | 0.75 | 0.15 | -0.45 | -0.95 | 0.5 | Amarillo | 0 | ||
| Puebla | $\dot{R}_{a21}$ | $\Phi_{+ \atop {a21}}$ | 0.85 | 0.525 | 0.25 | 0 | 0.875 | ||
| $\Phi_{- \atop {a21}}$ | 0.15 | 0.475 | 0.75 | 1 | 0.125 | ||||
| $\Phi_{ \atop {a21}}$ | 0.7 | 0.05 | -0.5 | -1 | 0.75 | Verde | -1 | ||
| Querétaro | $\dot{R}_{a22}$ | $\Phi_{+ \atop {a22}}$ | 0.825 | 0.525 | 0.275 | 0.025 | 0.825 | ||
| $\Phi_{- \atop {a22}}$ | 0.15 | 0.475 | 0.725 | 0.975 | 0.15 | ||||
| $\Phi_{ \atop {a22}}$ | 0.675 | 0.05 | -0.45 | -0.95 | 0.675 | Verde | -1 | ||
| Quintana Roo | $\dot{R}_{a23}$ | $\Phi_{+ \atop {a23}}$ | 0.85 | 0.575 | 0.275 | 0 | 0.8 | ||
| $\Phi_{- \atop {a23}}$ | 0.15 | 0.425 | 0.725 | 1 | 0.2 | ||||
| $\Phi_{ \atop {a23}}$ | 0.7 | 0.15 | -0.45 | -1 | 0.6 | Amarillo | -1 | ||
| San Luis Potosí | $\dot{R}_{a24}$ | $\Phi_{+ \atop {a24}}$ | 0.95 | 0.55 | 0.25 | 0 | 0.75 | ||
| $\Phi_{- \atop {a24}}$ | 0.05 | 0.45 | 0.75 | 1 | 0.25 | ||||
| $\Phi_{ \atop {a24}}$ | 0.9 | 0.1 | -0.5 | -1 | 0.5 | Amarillo | -1 | ||
| Sinaloa | $\dot{R}_{a25}$ | $\Phi_{+ \atop {a25}}$ | 0.85 | 0.525 | 0.275 | 0 | 0.85 | ||
| $\Phi_{- \atop {a25}}$ | 0.15 | 0.475 | 0.725 | 1 | 0.15 | ||||
| $\Phi_{ \atop {a25}}$ | 0.7 | 0.05 | -0.45 | -1 | 0.7 | Verde | -1 | ||
| Sonora | $\dot{R}_{a26}$ | $\Phi_{+ \atop {a26}}$ | 0.8 | 0.55 | 0.25 | 0 | 0.9 | ||
| $\Phi_{- \atop {a26}}$ | 0.2 | 0.45 | 0.75 | 1 | 0.1 | ||||
| $\Phi_{ \atop {a26}}$ | 0.6 | 0.1 | -0.5 | -1 | 0.8 | Verde | -1 | ||
| Tabasco | $\dot{R}_{a27}$ | $\Phi_{+ \atop {a27}}$ | 0.8625 | 0.525 | 0.25 | 0 | 0.8625 | ||
| $\Phi_{- \atop {a27}}$ | 0.1375 | 0.475 | 0.75 | 1 | 0.1375 | ||||
| $\Phi_{ \atop {a27}}$ | 0.725 | 0.05 | -0.5 | -1 | 0.725 | Verde | -1 | ||
| Tamaulipas | $\dot{R}_{a28}$ | $\Phi_{+ \atop {a28}}$ | 0.8 | 0.525 | 0.25 | 0 | 0.925 | ||
| $\Phi_{- \atop {a28}}$ | 0.2 | 0.475 | 0.75 | 1 | 0.075 | ||||
| $\Phi_{ \atop {a28}}$ | 0.6 | 0.05 | -0.5 | -1 | 0.85 | Verde | -1 | ||
| Tlaxcala | $\dot{R}_{a29}$ | $\Phi_{+ \atop {a29}}$ | 0.825 | 0.55 | 0.25 | 0 | 0.875 | ||
| $\Phi_{- \atop {a29}}$ | 0.175 | 0.45 | 0.75 | 1 | 0.125 | ||||
| $\Phi_{ \atop {a29}}$ | 0.65 | 0.1 | -0.5 | -1 | 0.75 | Verde | -1 | ||
| Veracruz | $\dot{R}_{a30}$ | $\Phi_{+ \atop {a30}}$ | 0.85 | 0.55 | 0.275 | 0.025 | 0.8 | ||
| $\Phi_{- \atop {a30}}$ | 0.15 | 0.45 | 0.725 | 0.975 | 0.2 | ||||
| $\Phi_{ \atop {a30}}$ | 0.7 | 0.1 | -0.45 | -0.95 | 0.6 | Amarillo | -1 | ||
| Yucatán | $\dot{R}_{a31}$ | $\Phi_{+ \atop {a31}}$ | 0.925 | 0.575 | 0.275 | 0 | 0.725 | ||
| $\Phi_{- \atop {a31}}$ | 0.075 | 0.425 | 0.725 | 1 | 0.275 | ||||
| $\Phi_{ \atop {a31}}$ | 0.85 | 0.15 | -0.45 | -1 | 0.45 | Amarillo | -1 | ||
| Zacatecas | $\dot{R}_{a32}$ | $\Phi_{+ \atop {a32}}$ | 0.9125 | 0.55 | 0.275 | 0 | 0.7375 | ||
| $\Phi_{- \atop {a32}}$ | 0.0625 | 0.45 | 0.725 | 1 | 0.2375 | ||||
| $\Phi_{ \atop {a32}}$ | 0.85 | 0.1 | -0.45 | -1 | 0.5 | Amarillo | -1 |
Analizando los resultados en términos de los colores asignados por el método FlowSort y la diferencia con respecto a los asignados mediante la metodología utilizada por la Secretaría de Salud, de la misma tabla 6, tenemos que solo se observan cinco coincidencias (diferencia cero), estos son: Chiapas, Coahuila, Durango, Guanajuato y Oaxaca. El resto de los estados presentan la diferencia de -1 en el color, esto es, en apariencia, el método FlowSort les asigna a esos estados un color más permisivo que el que les fue asignado por la metodología de la SS.
Sin embargo, hay que señalar que esta comparación entre los resultados de ambas metodologías no es del todo precisa. Adicionalmente a las diferencias de los fundamentos metodológicos de ambas, hay dos factores que inciden de manera fundamental en estos resultados. Por un lado, se encuentran las diferencias en las ponderaciones asignadas a cada indicador (o criterio), como ya se mencionó, no hubo manera de encontrar los valores de los pesos que la SS asigna el conjunto de los 10 indicadores utilizados, esto dificultado aún más por el paro de labores derivado de la pandemia, en las distintas oficinas donde se podrían consultar los datos. Por otra parte, en la metodología de la SS se consideran ajustes a las puntuaciones de los distintos indicadores en los estados, procedentes de diálogos y precisiones mantenidas con las autoridades locales de las entidades. Tampoco hubo manera de conseguir los detalles numéricos de tales ajustes.
Finalmente, no obstante las limitantes ya señaladas, se debe mencionar al menos una de las características relevantes del método FlowSort que pueden ser considerada en futuras aplicaciones y que pueden enriquecer el proceso de clasificación de las entidades en los colores del semáforo COVID-19: la metodología FlowSort ofrece la oportunidad de utilizar un conjunto de al menos seis funciones de preferencia que permiten fortalecer la participación de los tomadores de decisiones mediante la definición de umbrales de indiferencia y preferencia (Brans & Vincke, 1985). En este trabajo se utilizó solo la función de preferencia más simple, función usual (figura 1).
Conclusiones
De los resultados obtenidos, queda demostrada la factibilidad de utilizar el método FlowSort, como un método alternativo, en la clasificación por colores del Semáforo COVID-19 proporcionada por la Secretaría de Salud del gobierno mexicano. Asimismo, además de ser una alternativa sólida respaldada por la amplia cantidad y variedad de aplicaciones útiles reportadas por la literatura científica, esta permite la posibilidad de enriquecer la participación de los tomadores de decisiones mediante la utilización de distintas funciones de preferencia en cada uno de los indicadores considerados.
Referencias
Brüggemann, R. & Patil G. P. (2011). Ranking and prioritization for multi-indicator systems introduction to partial order applications. New York, Dordrecht Heidelberg London.Springer Sciences & Business Media.
Cavanna, J. M. (2019). El Semáforo de Eliminación de la Pobreza. Banco de desarrollo de América Latina y Fundación Paraguay. Paraguay.
Cori, A., Ferguson, N. M., Fraser, C., & Cauchemez, S. (2013). A new framework and software to estimate time-varying reproduction numbers during epidemics. American journal of epidemiology, 178(9) 1505-1512.
De la Cruz-Reyna, S., & Tilling, R. I. (2008). Scientific and public responses to the ongoing volcanic crisis at Popocatépetl Volcano, Mexico: importance of an effective hazards-warning system. Journal of Volcanology and Geothermal Research, 170(1-2) 121-134.
Ducrot, P., Julia, C., Méjean, C., Kesse-Guyot, E., Touvier, M., Fezeu, L. K., … & Péneau, S. (2016). Impact of different front-of-pack nutrition labels on consumer purchasing intentions: a randomized controlled trial. American journal of preventive medicine, 50(5) 627-636.
Enjolras, M., Camargo, M., & Schmitt, C. (2020). Evaluating Innovation and Export Capabilities of SMEs: Toward a Multi-Criteria Decision-Making Methodology. Journal of technology management & innovation, 15(3) 17-32.
European Centre for Disease Prevention and Control. 2021. Maps in support of the Council Recommendation on a coordinated approach to travel measures in the EU (europa.eu).
Fajardo, A. L. (2019). Gestión de crisis en la industria, asociada a la pandemia COVID-19. Revista Internacional Pienso en Latinoamérica, 2 (6) 45 – 55.
García, A. J. (2020). Síndrome de burnout en personal de salud durante la pandemia COVID-19: un semáforo naranja en la salud mental. Revista Salud Uis, 52(4) 432-439.
Jones, N. K., Ramsay, I., Moore, E., Fuld, J., Adcock, C., Banham-Hall, E., … & Mok, H. P. (2021). Admission COVID-19 clinical risk assessment for guiding patient placement and diagnostic testing strategy. Clinical Medicine, 21(2) 1-4.
Ishizaka, A., and P. Nemery. (2013). Multi-Criteria Decision Analysis: Methods and Software. Wiley editorial. Chichester West Sussex, United Kingdom.
Kao, H., Eaton, D. W., Atkinson, G. M., Maxwell, S., & Mahani, A. B. (2016). Technical meeting on the traffic light protocols (TLP) for induced seismicity: Summary and recommendations. Geological Survey of Canada, Open File, 8075, 20 p. doi:10.4095/299002
Larichev, O.I. (2001). Ranking multicriteria alternatives: The method ZAPROS III. European Journal of Operational Research, 131(3) 550-558.
Moheimani, A., Sheikh, R., Hosseini, S. M. H., & Sana, S. S. (2021). Assessing the agility of hospitals in disaster management: application of interval type-2 fuzzy Flowsort inference system. Soft Computing, 25(5) 3955-3974.
Montiel, A. L. F. (2019). Gestión de crisis en la industria, asociada a la pandemia COVID-19. Revista Internacional de PIENSO en Latinoamérica, 2(6) 45-55.
Nemery, P., & Lamboray, C. (2008). Flowsort: A flow-based sorting method with limiting or central profiles. TOP, 16 (1) 90–113.
Pelissari, R., Oliveira, M. C., Amor, S. B., & Abackerli, A. J. (2019). A new FlowSort-based method to deal with information imperfections in sorting decision-making problems. European Journal of Operational Research, 276(1) 235-246.
Pinzón, A., Gómez, P., & Romero, I. (2015). Esquema de los semáforos: una estrategia de evaluación formativa para compartir metas. RECME-Revista Colombiana de Matemática Educativa, 1(1) 66-71.
Rahmanimanesh, M., Shafiei Nikabadi, M., Pourkarim, F., & Davoodifar, G. (2017). Using Fuzzy Flowsort Inference System to Rank the Factors Leading to Failure for ERP Projects among Iranian Enterprises. Journal of Information Technology Management, 9(4) 787-808.
Rojo Guadalupe, Volman Víctor, y Braga Federico. 2020. Semáforo epidemiológico municipal. Argentinos por la educación, 1-14.
Sarrazin, R., De Smet, Y., & Rosenfeld, J. (2018). An extension of PROMETHEE to interval clustering. Omega. 80 12–21. doi: /10.1016/j.omega.2017.09.001
Schultz, R., Beroza, G., Ellsworth, W., & Baker, J. (2020). Risk‐Informed Recommendations for Managing Hydraulic Fracturing–Induced Seismicity via Traffic Light Protocols. Bulletin of the Seismological Society of America, 110(5) 2411-2422.
Secretaría de Salud. (2020). Lineamientos para la estimación de riesgos del semáforo por regiones COVID-19. Gobierno de México.
Sepúlveda, J. M., & Derpich, I. S. (2014). Automated reasoning for supplier performance appraisal in supply chains. Procedia Computer Science, 31, 966-975.
Shakya, D. R., Thapa, S. B., Kar, S. K., Sharma, V., Uchida, N., Ortiz, M. R., … & Bhattarai, P. R. (2020). COVID-19 across Countries: Situation and Lessons for Pandemic control. Journal of BP Koirala Institute of Health Sciences, 3(1) 9-27.
Spronk J., Steuer R.E., Zopounidis C. (2016) Multicriteria Decision Aid/Analysis in Finance. In: Greco S., Ehrgott M., Figueira J. (eds) Multiple Criteria Decision Analysis. International Series in Operations Research & Management Science, vol 233. Springer, New York, NY. https://doi.org/10.1007/978-1-4939-3094-4_24
Vizcaychipi, M. P., Shovlin, C. L., McCarthy, A., Howard, A., Brown, A., Hayes, M., … & Keays, R. T. (2020). Development and implementation of a COVID-19 near real-time traffic light system in an acute hospital setting. Emergency Medicine Journal, 37(10) 630-636.
