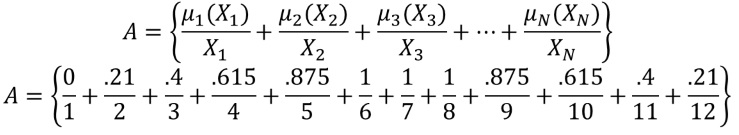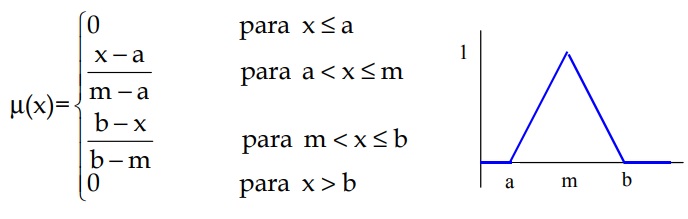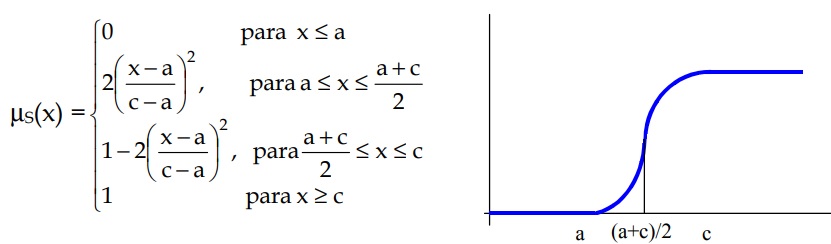Lógica Difusa

La lógica difusa, es una lógica que permite llegar a conclusiones “razonadas” a partir de información ambigua o imprecisa. Este concepto fue desarrollado por el profesor Lofti A. Zadeh (1965), trabajo retomado en Zadeh (1996), quien la presentó como una forma de interpretar información basada en la pertenencia parcial de tal información con respecto a un determinado tipo de conjuntos, definidos como conjuntos difusos.

Uno de los grandes aportes de esta lógica, es que permite modelar situaciones o comportamientos que son vagos en sí mismos, es decir, se adapta mejor a la realidad que una lógica clásica, en dónde solo existen dos valores a decidir. Por ejemplo, si consideramos un clima frío a 10° C y un clima caliente a 30° C, bajo una perspectiva clásica, sólo se tendría el valor frío y caliente, sin embargo, entre estos valores existen muchas otras temperaturas que tienen ambigüedad con respecto a los valores definidos, es decir bajo una lógica clásica, ¿20°C, es una temperatura fría o caliente?, bajo esta perspectiva, no se tiene certeza de a qué conjunto pertenece 20° C, pero si esta situación se analiza bajo una perspectiva difusa, es posible definir la pertenencia de 20 grados con respecto al conjunto de las temperaturas frías y al de las temperaturas calientes. Esta situación, puede observarse en la figura 1, en la cual tenemos por un lado, la lógica clásica, se puede observar que si se evalúan los valores  X y Y, sólo pueden pertenecer a un conjunto lógico cada uno, sin embargo, en la lógica difusa, estos mismos valores pueden tener diferentes rangos de pertenencia con respecto a los conjuntos difusos, si se evalúa el valor X, este tiene una pertenencia del 10% con respecto al conjunto caliente y una pertenencia del 30% con respecto al conjunto frío, es decir, el valor X es un poco más frío que caliente; por otro lado, si se evalúa el valor Y, es posible ver que este tiene una pertenencia del 80% con respecto al conjunto caliente.

En esta misma figura, podemos ver que desde el inicio de los conjuntos hasta su punto máximo, el 100%, se generan pendientes de pertenencia, está pendiente indica la vaguedad de un dato con respecto a un conjunto. Existe un conjunto caliente y uno frío, pero las temperaturas no son solo completamente calientes o completamente frías, tienen rangos de pertenencia.

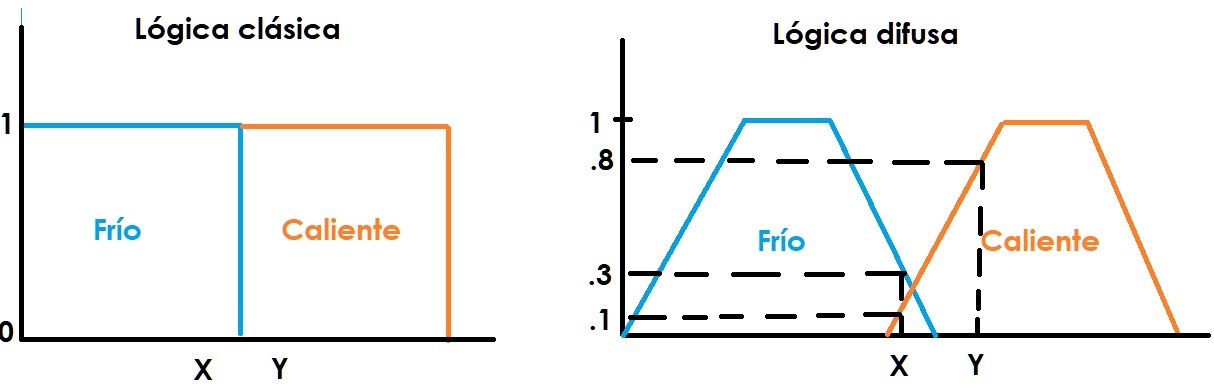Fig.1.- Diferencias entre conjuntos de lógica clásica y lógica difusa.

Es importante notar que el razonamiento humano no reacciona en una manera de lógica clásica, sino que por el contrario, evalúa el entorno y en función de las ponderaciones de cada una de las variables toma una decisión, por lo que la lógica difusa es más adecuada para tratar de emular tal comportamiento mental.

Algo relevante de la lógica difusa, es que ella ha servido para el desarrollo de una cantidad incontable de aplicaciones de todo tipo tales como medicina y bioinformática (Torres & Nieto, 2006), aplicaciones industriales (Larsen, 1980), robots autónomos (Peri  & Simon, 2005), controladores de motores de inducción (Uddin et al., 2002), entre muchas otras.

En base a la lógica difusa, se han generado los controladores difusos, que son en sí mismos un tema aparte de analizar, y que en otra sección de esta web, serán tratados.

Conjuntos difusos

Un conjunto difuso se puede definir en la siguiente forma:

$$A={\{(X,\mu_A(X))| X\in U}\}$$

Donde  $A$ está formado por todos los pares ordenados $X$ y el resultado de la función de pertenencia $\mu_A(X)$ para todo elemento dentro del universo de discurso $U$.

Podemos expresar un conjunto $A$, de forma discreta en la manera:

$$A=\sum_U {\mu_A(X_i)\over {X_i}}$$

Y de forma continua por medio de:

$$A=\int_{U}  {\mu_A(X_i)\over {X_i}} $$

 

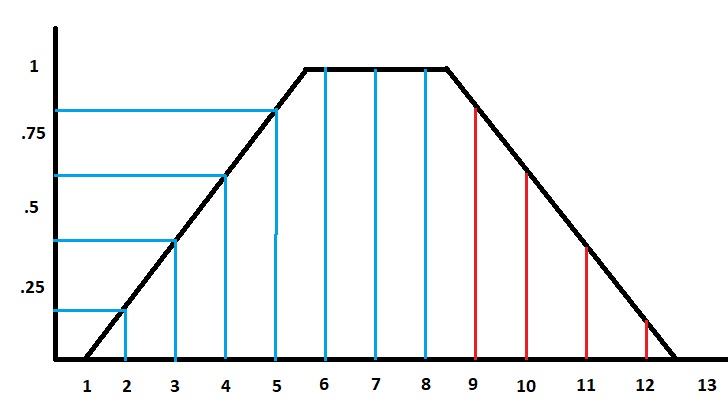
Por ejemplo, tenemos el conjunto difuso de la siguiente figura:

Fig 2.- Conjunto difuso de prueba.

Y su representación discreta está definida por la siguiente expresión:

Funciones de pertenencia

Existen diferentes tipos de conjuntos difusos que pueden ser utilizados para el modelaje de diferentes fenómenos o comportamientos, sin embargo, existen algunos de estos que son más comúnmente utilizados, debido principalmente a su facilidad de computación o que son funciones que fácilmente pueden representar un comportamiento difuso. Entre los conjuntos, o funciones, más utilizados están los siguientes:

Función Gamma, representada en la siguiente forma:

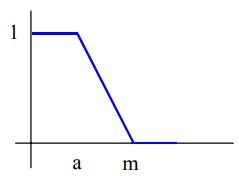
Función L, que puede describirse como el inverso de la función Gamma:

Función triangular, que se representa de la siguiente manera:

Función trapezoidal, la función más popular, representada por:

Función sigmoidea, dada por:

Referencias

Larsen, P. M. (1980). Industrial applications of fuzzy logic control. International Journal of Man-Machine Studies, 12(1), 3-10.

Peri, V. M., & Simon, D. (2005, June). Fuzzy logic control for an autonomous robot. In NAFIPS 2005-2005 Annual Meeting of the North American Fuzzy Information Processing Society (pp. 337-342). IEEE.

Torres, A., & Nieto, J. J. (2006). Fuzzy logic in medicine and bioinformatics. journal of Biomedicine and Biotechnology, 2006.

Uddin, M. N., Radwan, T. S., & Rahman, M. A. (2002). Performances of fuzzy-logic-based indirect vector control for induction motor drive. IEEE Transactions on Industry applications, 38(5), 1219-1225.

Zadeh, L. A. (1965). Information and control. Fuzzy sets, 8(3), 338-353.

Zadeh, L. A. (1996). Fuzzy sets. In Fuzzy sets, fuzzy logic, and fuzzy systems: selected papers by Lotfi A Zadeh (pp. 394-432).