Transformada wavelet
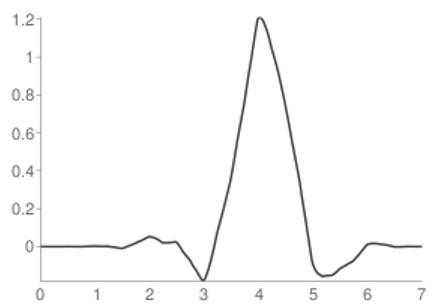
Las wavelets son señales, o formas de onda, las cuales tienen una duración limitada y un valor promedio de cero. Las wavelets pueden ser irregulares y asimétricas, características que les otorgan una mejor adaptación en el análisis de señales en comparación con la transformada de Fourier. Existen muchos tipos de wavelets como la wavelet Haar, la familia de wavelets Daubechies, la wavelet sombrero mexicano, la wavelet Symlet, etc. La figura 1, muestra una de las wavelets más populares, la Symlet 4.
Fig. 1.- Wavelet Symlet 4 o Sym 4.
Para ver una colección de diferentes familias de wavelets, se pueden dirigir al trabajo de Elena Pinto Moreno, que da una colección muy completa:
https://e-archivo.uc3m.es/bitstream/10016/16582/1/PFC_Elena_Pinto_Moreno_Anexos.pdf
La elección de una wavelet dependerá del tipo de señal que se pretenda analizar, así como la información que se quiera obtener de ella. Podemos seguir dos criterios para la selección de la wavelet. El primero consiste en buscar varias wavelets que tengan una forma parecida a nuestra señal y el segundo se basa en realizar pruebas con diferentes wavelets seleccionando aquella que obtenga los mejores resultados.
La wavelet elegida, para implementar la transformada wavelet a una señal, se le asigna el nombre de wavelet madre. Se le conoce como wavelet madre ya que será esta la que sufra algunas modificaciones para realizar el análisis: se expandirá o se comprimirá, y se trasladará a lo largo de la señal. Estas modificaciones están a cargo de los parámetros de escalamiento y desplazamiento. En el escalamiento se alarga o se comprime la wavelet, lo que nos permite ver tanto los detalles como los componentes de la señal de forma global. Mientras que el desplazamiento se refiere al recorrido de la wavelet a lo largo de la señal. Podemos definir a la wavelet madre $\psi_{a,b} (t)$ , añadiéndole los parámetros de escalamiento y de desplazamiento, mediante la siguiente fórmula:
$$\psi_{a,b}(t)=\frac{1}{\sqrt{a}}\cdot\psi\left(\frac{t-b}{a}\right)$$
donde $a$ es el escalamiento y $b$ es el desplazamiento.
De forma general la transformada wavelet descompone una señal mediante el uso de las versiones escaladas y desplazadas de la wavelet madre. Podemos decir que la wavelet actúa como un filtro pasa banda el cual solo permite el paso de ciertos componentes de la señal a una determinada frecuencia.
Existen distintos tipos de transformada wavelet como lo son la transformada wavelet continua, la transformada wavelet discreta y la transformada wavelet packet. A continuación, se explicarán las dos primeras.
La transformada wavelet continua (CWT) se define como la suma de la multiplicación de una señal continua y la wavelet madre en su forma desplazada y escalada $\psi_{a,b} (t)$. Tiene la forma:
$$CWT(a,b)=\frac{1}{\sqrt{a}}\int_{-\infty}^{\infty} x(t)\psi\left(\frac{t-b}{a}\right)dt$$
donde $X(t)$ es la señal continua.
Los parámetros de escalamiento y desplazamiento dan paso a la obtención de los coeficientes wavelet. Los coeficientes wavelet nos indican cuanta relación hay entre la señal y la wavelet madre. Esta relación nos permite conocer los componentes frecuenciales de la señal.
La transformada wavelet discreta (DWT) se obtiene al discretizar los parámetros de desplazamiento y escalamiento dentro de la transformada wavelet continua. Usualmente los valores que se implementan para realizar esto son:
$$a=2^{-j}$$
$$b=k2^{-j}$$
donde $a$ es el escalamiento, $b$ es el desplazamiento y $j, k$ deben ser valores enteros.
Definidos los parámetros de escalamiento y desplazamiento con valores discretos, la wavelet madre toma la forma:
$$\psi_{j,k}(t)=2^{\frac{j}{2}}\psi\left(2^{j}t-k\right); j,k\in Z$$
Esto último permite definir la transformada wavelet discreta como:
$$DWT_{j,k}=2^{\frac{j}{2}}\int_{-\infty}^{\infty} x(t)\psi\left(2^{j}t-k\right)dt$$
donde $X(t)$ es una señal discreta.
La transformada wavelet discreta nos permite reconstruir la señal una vez que calculamos los coeficientes wavelet. Para realizar esta reconstrucción se necesita de dos funciones: la función wavelet $\psi (t)$ y $\phi (t)$ la función escala . La reconstrucción de la señal se obtiene mediante la siguiente ecuación:
$$x(t)=\sum_{k}\sum_{j}c_{j,k}\phi (t)+\sum_{k}\sum_{j}d_{j,k}\psi (t); j,k\in Z$$
Donde $c_{j,k}$ son los coeficientes de escala o de aproximación y $d_{j,k}$ representa los coeficientes wavelet o de detalle. Cabe mencionar que los coeficientes de aproximación están asociados con la función escala, mientras que los coeficientes de detalle lo están con la función wavelet.
Los coeficientes de aproximación y de detalle nos permiten obtener información sobre las características de la señal, además con su manipulación podemos obtener una nueva señal eliminando componentes no deseados de la señal original.
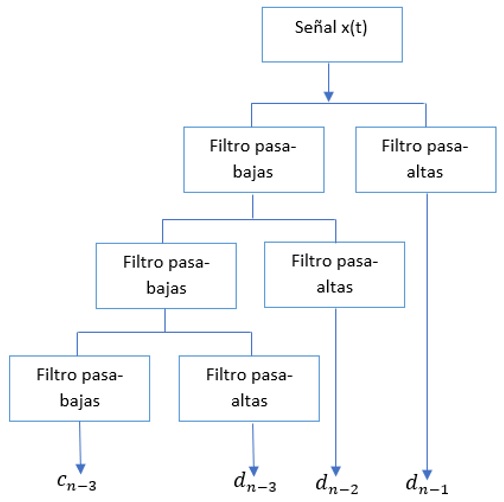
El desarrollo de algoritmos para evaluar el DWT condujo a la implementación de “bancos de filtros“. Estos filtros corresponden a un filtro pasa bajo y un filtro pasa alto, cuando la señal original pasa a través de tales filtros, se obtienen los coeficientes de salida $c_{j,k}$ y $d_{j,k}$ respectivamente. Se puede obtener una descomposición de una señal a diferentes niveles pasando los coeficientes de escala obtenidos del filtrado anterior por un par de filtros idénticos, obteniendo así los coeficientes del siguiente nivel. La figura 2 representa este proceso.
Fig. 2.- Proceso de filtrado de una señal para la extracción de características, cada par de filtros en un determinado nivel, genera los coeficientes que serán pasados al siguiente nivel.
La obtención de tales coeficientes debido a que, ya sea con su uso o su manipulación las características que describen una señal pueden ser obtenidas.