Recursividad
Un aspecto por demás interesante que representa el comportamiento de diferentes y variados fenómenos es la recursividad. La recursividad puede definirse como el proceso por el cual una función se llama a sí misma para resolver un problema, este concepto puede verse como un proceso que puede repetirse hasta el infinito si no es detenido en un nivel recursivo definido. Ciertos problemas grandes, tienen la característica de que pueden ser representados como la descomposición de problemas más pequeñas, siendo estos problemas pequeños una réplica del problema principal. Algunos problemas matemáticos que pueden ser resueltos por este tipo de métodos son los factoriales, la serie de Fibonacci, las torres de Hanoi, y los fractales, entre otros. En la figura 1, podemos ver la representación del fractal llamado “El copo de nieve de Koch”, como podemos visualizar, la generación del copo parte de un triángulo, al que se le superpone otro triangulo invertido, a cada nuevo triangulo se le superpone nuevamente un triángulo de su mismo tamaño, generando una superposición infinita en un proceso netamente recursivo.
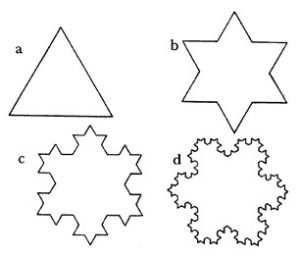
Fig. 1. El copo de nieve de Koch, fractal de generación recursiva.
Árboles binarios
Los árboles binarios (AB) son estructuras de datos abstractas y no lineales. Los AB están compuestos de un conjunto finito de elementos (Nodos), cada uno de estos nodos almacena un dato y a su vez puede apuntar hacia dos nodos más, el sub árbol izquierdo y el sub árbol derecho. En la figura 1, podemos observar la representación de un árbol binario.
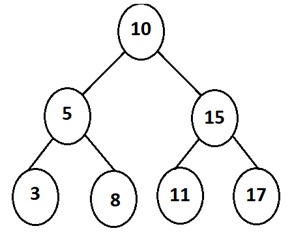
Fig 2.- Representación de un árbol binario.
Como se puede apreciar en la figura 2, los AB son estructuras inherentemente recursivas, ya que cada sub nodo presenta el mismo comportamiento que el nodo anterior.
Los AB pueden ser recorridos de diferentes formas (Preorden, Inorden, Postorden) para poder localizar algún dato definido que se encuentre almacenado en él.
Una característica importante de estas estructuras, es que los datos que están almacenados en ellas, pueden ser eliminados, modificados, o incluso, se pueden agregar nuevos datos. Por los motivos descritos, estas estructuras pueden ser utilizadas en una gran cantidad de aplicaciones computacionales, entre las que se encuentra la gestión de grandes cantidades de datos (Power & Zanna, 1995) y el desarrollo de juegos (Adel et al., 1975).
Como ya se mencionó, este tipo de esquemas tiene tres maneras básicas en las cuales se pueden recorrer sus nodos: Preorden, Inorden y posorden. Cada de una de estas formas de recorrer el árbol se define en base a su secuencia de recorrido. En el caso del preorden, se recorre primero la Raíz, después el lado derecho del nodo para concluir por el recorrido de su lado izquierdo; en el caso del Inorden, tenemos que primero se recorre la rama derecha del nodo, sigue la raíz y concluye con su rama izquierda; y por último tenemos el posorden, en dónde primero se recorre la rama derecha del nodo, luego la rama izquierda, y concluye con la raíz.
Fractales para descargar
Existe una gran cantidad de fractales que pueden ser programados de forma sencilla y que se ven atractivos en su funcionamiento, entre ellos se encuentra el árbol de Pitágoras, que se puede ver en la siguiente figura:
Fig. 3.- Fractal llamado Árbol de Pitágoras, que presenta una recursividad de nivel 12.
Para poder dibujar este árbol, se puede descargar el siguiente script de Python, este puede ser ejecutado en línea a través de la página http://www.pythonsandbox.com/turtle
En el siguiente vídeo, se muestra la ejecución del script anterior, cuando se selecciona un nivel 12 de recursividad:
Otro fractal de gran belleza, es la flor que se muestra en la siguiente figura:
Fig. 4.- Fractal que representa a un aflor.
El script para dibujar tal fractal, se puede obtener del siguiente enlace, y puede ejecutarse en la página https://trinket.io/turtle:
La ejecución de este script, puede verse en el siguiente vídeo:
Para la realización de árboles fractales más complejos que los mencionados en esta página, se puede consultar el archivo siguiente, el cual utiliza Turtle de Python.
Referencias
Powers, F. A., & Zanarotti, S. R. (1995). U.S. Patent No. 5,442,784. Washington, DC: U.S. Patent and Trademark Office.
Adelson-Velskiy, G. M., Arlazarov, V. L., & Donskoy, M. V. (1975). Some methods of controlling the tree search in chess programs. Artificial Intelligence, 6(4), 361-371.



