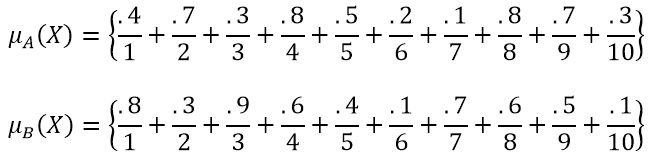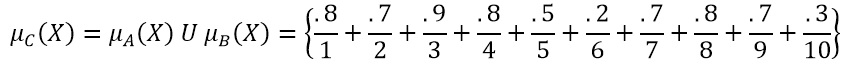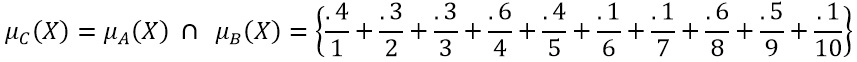Operaciones entre conjuntos difusos
Como en la lógica clásica, en la lógica difusa se pueden aplicar diferentes funciones básicas para trabajar con los conjuntos definidos. En este punto, sólo vamos a hablar de las tres operaciones base de la lógica: La unión, la intersección y el inverso. Desde un punto de vista subjetivo, se puede asegurar que el trabajar con estas operaciones sobre estos conjuntos es más fácil que trabajar sobre lógica clásica.
A continuación se presentan algunos ejemplos y explicaciones de cada una de estas operaciones:
Unión
La unión de dos conjuntos difusos µA (x) y µB (x), puede interpretarse como el valor máximo en el punto (x) de cada uno de ellos tal como se describe a continuación.
Esta función también es representada por la expresión lógica OR.
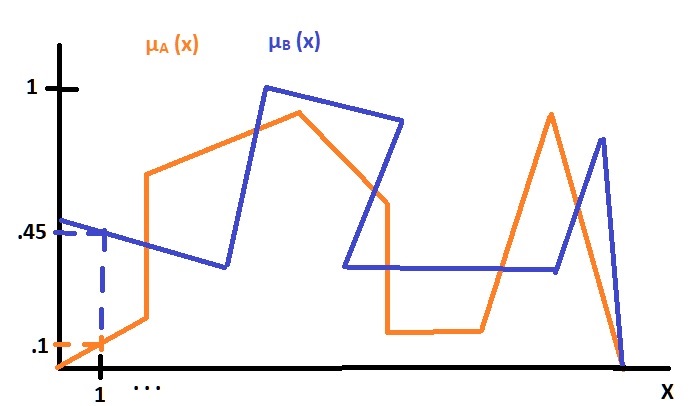
Suponemos que tenemos los conjuntos µA (x) y µB (x) que se muestran en la figura 1:
Fig. 1.- Conjuntos µA (x) y µB (x), utilizados como base para las operaciones de unión e intersección.
Ahora, a partir de ellos vamos a obtener:
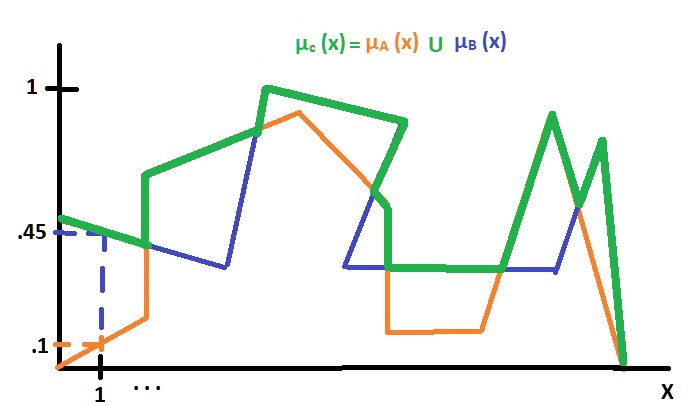
Quedando el conjunto verde µC (x) de la siguiente figura:
Fig. 2.- Unión de los conjuntos µA (x) y µB (x).
Como podemos observar en la figura 2, se fueron comparando en punto a punto los dos conjuntos, y de cada par de puntos comparados, se fue marcando el valor máximo.
Intersección
La intersección de dos conjuntos difusos µA (x) y µB (x), puede interpretarse como el valor mínimo en el punto (x) de cada uno de ellos tal como se describe a continuación.
Esta función también es representada por la expresión lógica AND.
Suponemos que tenemos los conjuntos µA (x) y µB (x) que se muestran en la figura 1 y a partir de ellos vamos a obtener:
Quedando como resultado el conjunto verde µC (x) de la figura 3:
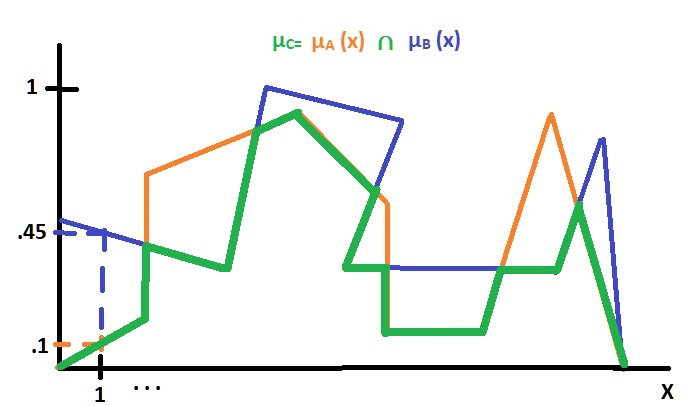Fig. 3.- Intersección de los conjuntos µA (x) y µB (x).
Como podemos observar en la figura 3, se fueron comparando en punto a punto los dos conjuntos, y de cada par de puntos comparados, se fue marcando el valor mínimo.
Inverso
El inverso de un conjunto difuso µA (x), puede obtenerse a través de la operación µB (x)=1- µA (x).
Suponemos que tenemos el conjunto µA (x) que se muestran en la figura 4 y a partir del conjunto anaranjado µA (x), obtenemos µB (x) =1- µA (x).
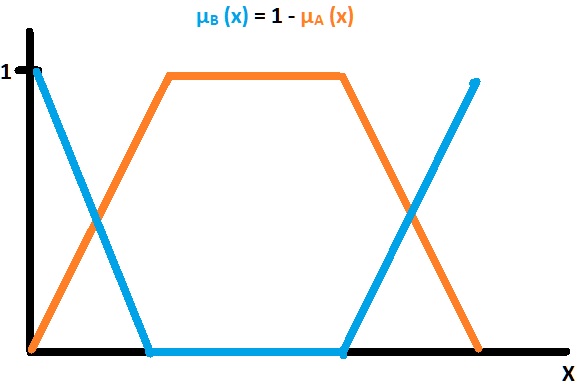Fig. 4.- Representación del inverso del conjunto difuso µA (x).
Operaciones numéricas
Las operaciones ya descritas, pueden ser realizadas de forma numérica, por ejemplo, tenemos los conjuntos µA (x) y µB (x) representados por:
A partir de los conjuntos anteriores, podemos obtener la unión de ambos:
Y en la misma forma, podemos obtener la intersección:
Como se puede observar en los ejercicios realizados, las operaciones de los conjuntos difusos son de gran sencillez y simplicidad.