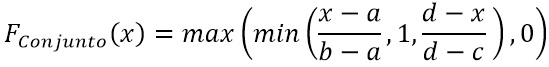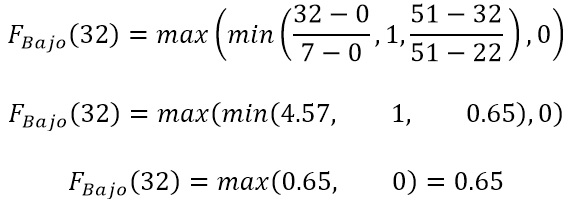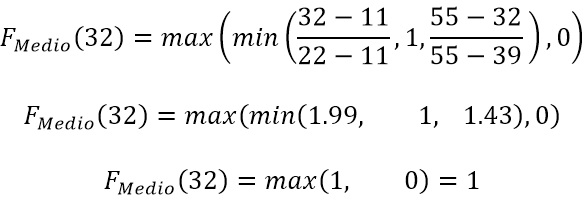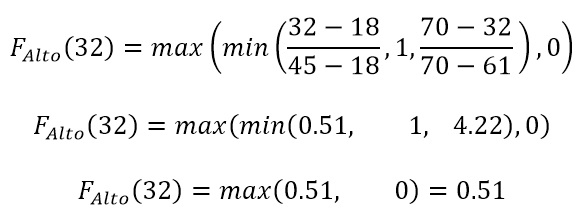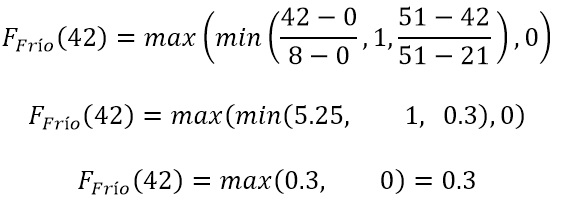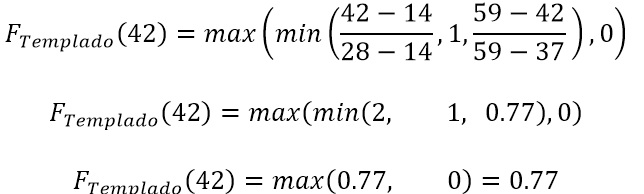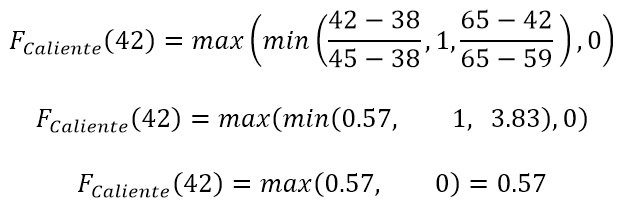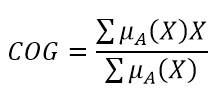Ejemplo de controlador difuso
Vamos a suponer que tenemos dos sensores que van a servir como entradas de nuestro sistema difuso, un sensor de temperatura y uno de humedad. Estos sensores servirán para controlar el porcentaje de riego de un sistema ficticio. Vamos a separar el universo de la temperatura en los conjuntos: frío, templado y caliente; y la humedad generará los conjuntos: bajo, medio y alto. Así mismo, la variable de salida será modelada con los conjuntos: mínimo, poco, regular y mucho. Hay que hacer la aclaración que estos conjuntos son definidos en función de las necesidades del sistema, así como también, deben de estar modelados de acuerdo a valores representativos reales del problema. En este caso, ni los valores, ni los conjuntos son netamente representativos del problema, debido a que se busca un ejercicio de ejemplificación en el cual se van a colocar valores de entrada “tramposos” para que sirvan al propósito de explicación.
Los conjuntos difusos representativos de las variables de entrada y el actuador de salida, los podemos ver en las siguientes imágenes.
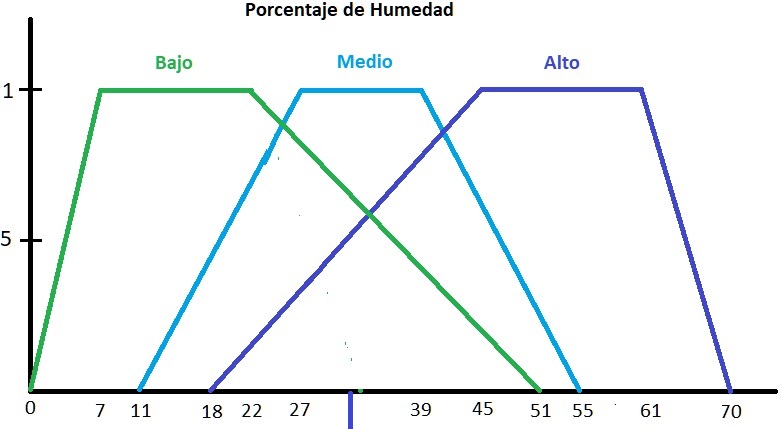
Fig. 1.- Conjuntos difusos en los que se separa la variable de entrada, Humedad.
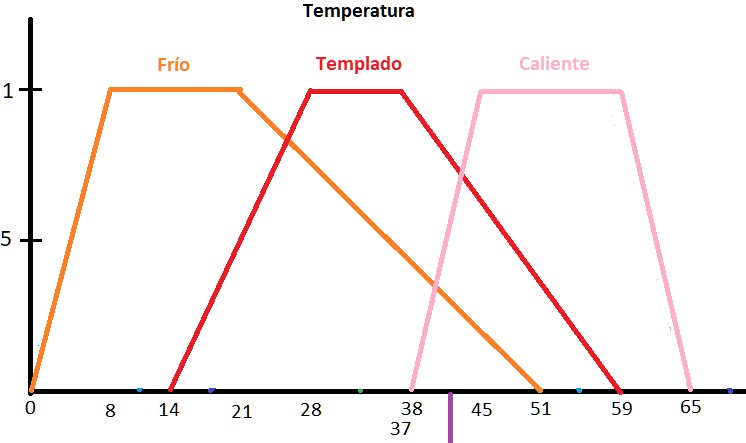
Fig. 2.- Conjuntos difusos en los que se separa la variable de entrada, Temperatura.
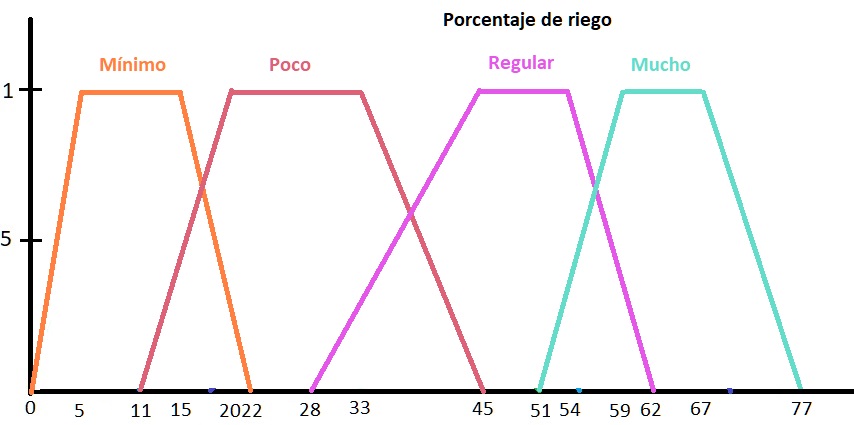
Fig. 3.- Conjuntos difusos en los que se separa la variable de salida, porcentaje de Riego.
Ahora bien, suponemos que en un determinado momento, los sensores de entrada captan los dos valores representados por las líneas moradas en las figuras 1 y 2, representando Temperatura= 42° y Porcentaje de humedad= 32%. Con estos valores de entrada, el controlador calculará el porcentaje de riego adecuado en la salida.
Primero que nada, es necesario calcular las relaciones de pertenencia del 32% de humedad en cada uno de los conjuntos en los que el valor de entrada impacta, correspondientes a la variable Humedad, para esto, consideramos las ecuaciones que representan al conjunto Trapezoidal, tal que:
Para x=32, en el conjunto Bajo, tenemos:
Ahora evaluamos x=32, en el conjunto Medio, tenemos:
Ahora evaluamos x=32, en el conjunto Alto, tenemos:
Si podemos observar en la figura que representa a la variable humedad, es posible corroborar que cada una de estas relaciones de pertenencia está de acuerdo con respecto al punto donde intersecta el valor de entrada x=32.
Ahora, es necesario realizar el mismo procedimiento con la entrada de 42° de la variable Temperatura.
Evaluamos x=42 en el conjunto Frío, tal que
Evaluamos x=42 en el conjunto Templado, tal que
Evaluamos x=42 en el conjunto Caliente, tal que
Una vez que se han obtenido todas las relaciones de pertenencia de las dos entradas, se genera un conjunto de reglas en la forma IF (Entrada 1 AND/OR Entrada2) THEN (Salida). Estas reglas deben de tener un sentido lógico con respecto al problema o fenómeno que se está modelando.
Vamos a generar estas reglas de acuerdo a la matriz de reglas que se muestra a continuación:
| Bajo | Medio | Alto | |
| Frío | R1= Poco | R2=Mínimo | R3= Mínimo |
| Templado | R4=Regular | R5=Regular | R6=Poco |
| Caliente | R7=Mucho | R8=Mucho | R9=Regular |
La matriz de reglas se puede leer en la siguiente forma, utilizando la celda superior izquierda como ejemplo, tenemos que si la temperatura está en el conjunto Frío y la humedad está en el conjunto Bajo, entonces la salida se encontrará en el conjunto Poco, colocado en otra forma IF (Frío AND Bajo THEN Poco), obviamente, repitiendo este proceso para cada una de las celdas de la matriz. Es importante mencionar que aunque aquí se utilizó AND, dependiendo de la naturaleza del problema, se puede utilizar OR.
Ahora se realizara el cálculo de estas reglas de forma numérica:
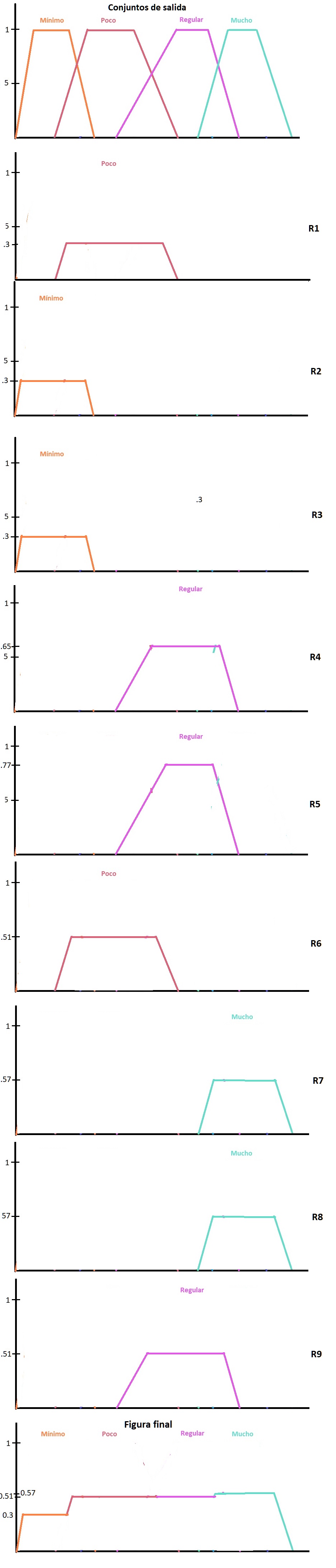
Con los valores obtenidos en las reglas, se puede generar el siguiente grupo de conjuntos difusos:
Fig. 4.- Conjuntos difusos obtenidos después de aplicar las reglas lógicas a las relaciones de pertenencia de los valores de entrada.
Para generar las gráficas mostradas en la figura 4, es necesario ver que, R1 es colocado en el conjunto Poco, debido a que en la matriz de reglas se especifica esta salida; y se coloca con una relación de pertenencia de 0.3, porque ese fue el cálculo numérico obtenido por medio de la intersección de los conjuntos utilizados en cada regla. Este procedimiento se realiza para cada regla.
Ahora, al final de la figura, tenemos una figura irregular que es la combinación de todas las reglas definidas, para obtener el valor de salida es necesario calcular el centroide, o centro de gravedad, de la gráfica por medio de:
Debido a la gran cantidad de puntos que presenta la imagen de salida, este resultado lo obtendremos directamente de este mismo modelo realizado en Matlab, ingresando los dos valores de entrada, obtenemos que la salida es igual a 41.5% de capacidad de riego.
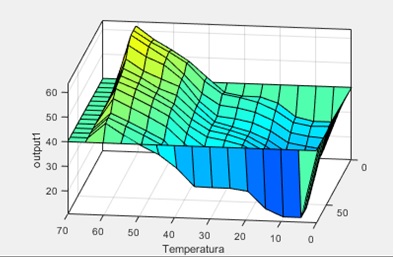
La superficie de acción del controlador diseñado se puede ver en la figura 5:
Fig. 5.- Superficie de acción del controlador diseñado, imagen generada por medio de Matlab.
Para poder verificar este controlador, se puede descargar el siguiente archivo .FIS y ejecutarlo en Matlab, en él se encuentra el mismo controlador modelado en esta página.