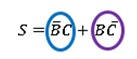Mapas de Karnaugh

Los mapas de Karnaugh son una herramienta utilizada para la simplificación de funciones lógicas booleanas y a diferencia de la resolución por algebra de Boole, este es un método gráfico que implica conocer las representaciones canónicas de las funciones.

El Mapa de Karnaugh tiene la característica de que puede ser visto como una representación bidimensional de una tabla de verdad. En la tabla de verdad, se colocan las variables por columnas y las combinaciones de tales variables determinan un valor de salida, 0 o 1, sin embargo, en el mapa las variables se colocan como si de un plano cartesiano se tratara, respetando cada una de las combinaciones que de ellas se generan, y colocando en la intersección de las combinaciones de las variables, el valor de salida.

Una de las ventajas de estos elementos gráficos, es que evitan la realización de cálculos algebraicos, y al determinar la función de salida, esta se encuentre minimizada.

Los mapas muestran la relación que existe entre las entradas y las salidas de un circuito lógico, si se aplica adecuadamente el resultado será el más simplificado posible. Pueden ser utilizados para cualquier número de variables de entrada sin embargo se recomienda un máximo de seis variables.

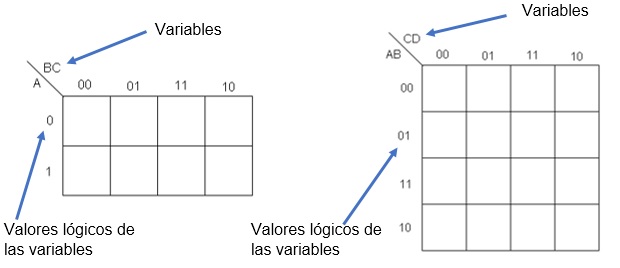
En la figura 1, vemos dos ejemplos de la representación de los mapas de Karnaugh, como ya se mencionó, se pueden utilizar más variables, pero en este caso nos enfocaremos en mapas con 3 y 4 variables.

Fig. 1.- Representación base de los mapas de Karnaugh, del lado izquierdo se tiene un mapa de tres variables, y del lado derecho se tiene un mapa de 4 variables. En los mapas se puede ver la forma de ordenar las variables y los valores lógicos que puede tener cada variable o combinación de variables.

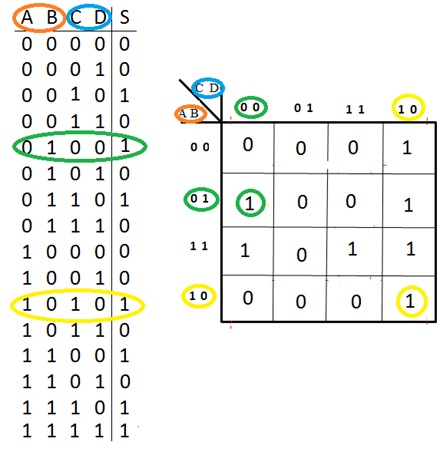
Como ya se mencionó, el mapa de Karnaugh es una representación en dos dimensiones de una tabla de verdad, en la figura 2 podemos ver la forma en la que una tabla de verdad es representada por un mapa.

Fig. 2.- Forma de pasar una tabla de verdad a un mapa de Karnaugh.

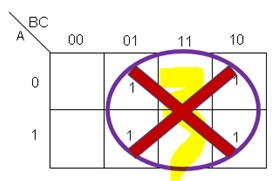
En la figura 2 se puede ver la forma de pasar una tabla de verdad a un mapa de Karnaugh, vemos que la tabla tiene 4 variables colocadas de la A a la D, ordenadas en columnas. Estas 4 variables forman diferentes combinaciones ($2^4=16$) y cada combinación tiene una salida lógica {0, 1}, por ejemplo la combinación en la tabla de verdad encerrada en amarillo puede ser representada como $A\bar{B}C\bar{D}$, esta es la representación canónica, es decir es una combinación involucra a todas las variables y que tiene como salida, en este caso, un 1. Hay que hacer notar que cuando el valor de la variable es 1, solo se representa con el nombre de la variable, sin embargo, cuando el valor de la variable es 0, se representa con la variable negada.

Se puede ver en la figura 2 que las variables A y B encerradas en anaranjado, son pasadas al mapa como si se tratara del eje de las Y de un plano cartesiano; las variables C y D son pasadas al mapa como si se tratara del eje de las X dentro del plano.

Ahora, para saber dónde colocar los valores vamos a utilizar la combinación enmarcada con verde, podemos ver que a las variables A y B les corresponden los valores 0 y 1 respectivamente, buscamos en el eje de las Y en donde se encuentra esa combinación de valores, lo podemos ver también enmarcado con verde; Para las variables C y D, se tienen los valores 0 y 0, por lo que buscamos en el eje de las X tal combinación, la cual también es marcada con verde, ahora el valor que le corresponde, en este caso 1, se coloca en la casilla donde ambas combinaciones se intersectan. Este mismo procedimiento se puede ver para la combinación enmarcada en amarillo. Obviamente, todas las casillas del mapa deben de ser llenadas en la misma forma.

Una vez definida la manera en la cual se llena un mapa, vamos a dar las reglas con las cuales se obtienen las funciones booleanas simplificadas. Estas funciones dependerán de la cantidad de 1’s o 0’s agrupados, y las posiciones del mapa en las que se encuentran. A continuación, se enlistan puntos importantes que deben tomarse en cuenta para la formación de grupos dentro del mapa de Karnaugh:

Los grupos deben contener una cantidad de elementos igual a potencias de 2. Es decir, los grupos solo podrán realizarse con cantidades de celdas iguales a: 1, 2, 4, 8, 16, 32, etc.
Se deben generar grupos con combinaciones de variables adyacentes, es decir, sólo debe de haber un cambio entre cada una de las combinaciones, por ejemplo la combinación $AB\bar{C}$ es adyacente con $A\bar{B}\bar{C}$, ya que sólo cambia la variable B.
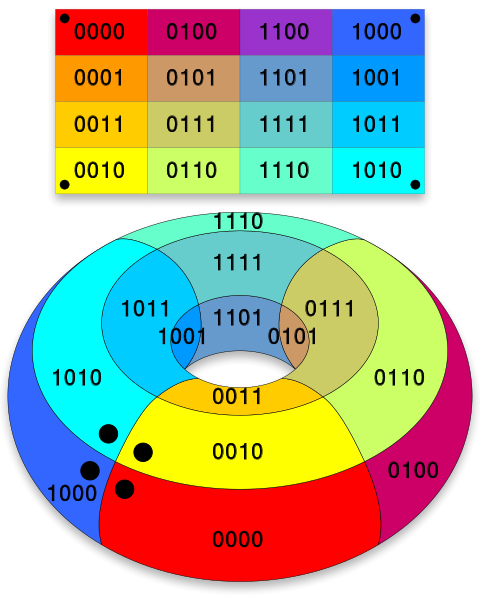
Grupos en las posiciones en los extremos y esquinas del mapa. Las posiciones de los extremos y las esquinas son adyacentes, por lo que se pueden agrupar. Esta adyacencia se debe a que el mapa de Karnaught puede ser visto como un toroide, tal como se ve e la figura 3.
Grupos de unos darán lugar a una suma de productos o mini términos.
Grupos de ceros darán lugar a un producto de sumas o maxi términos.
Los grupos deben ser lo más grande posible. Se buscará realizar grupos con la mayor cantidad de elementos posibles, entre más grande el grupo, se obtiene una función más simplificada.
No se pueden generar grupos en diagonal. Solo se permitirán grupos en vertical y horizontal dentro del mapa.
Puede existir solapamiento de grupos, siempre y cuando exista al menos un elemento que no haya sido agrupado anteriormente.
No deben existir grupos redundantes, es decir, no se puede realizar un grupo dentro de otro grupo, y no se puede realizar un grupo con elementos que ya hayan sido completamente agrupados en otros conjuntos.

Fig. 3.- Conversión de un mapa bidimensional a un toroide tridimensional, en donde se puede notar la adyacencia entre las esquinas y los extremos. Se pueden notar puntos negros en las 4 esquinas del mapa, y como estos puntos se juntan en el toroide. También es posible observar como la posición 0100 (Extremo superior del mapa) y la posición 0110 (Extremo inferior del mapa), se juntan en la representación toroideal. Figura recuperada de https://upload.wikimedia.org/wikipedia/commons/3/33/Karnaugh_map_torus.svg

Para la demostración de las reglas descritas, se utilizarán los siguientes ejemplos:

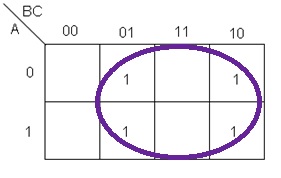
Ejemplo 1. Encontrar la función que representa al mapa de Karnaugh de la figura 4:

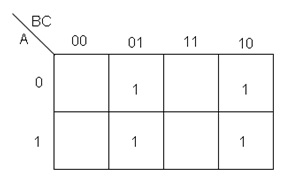Fig.4.- Primer ejemplo mapas de Karnaugh.

En este ejemplo se puede ver con facilidad el número de grupos que se podrán realizar, debes recordar que no es posible hacer grupos en diagonales y que se hacen con potencias de 2.

Como primera parte, vamos a ver un error que se puede cometer al resolver este tipo de casos en la figura 5:

Fig. 5.- Posible error a realizar en la resolución de un mapa, en a) se ve como se intenta generar un grupo aun cuando hay casillas vacías dentro del supuesto grupo, en b) se indican las casillas vacías así como una marca que indica el error.

No se pueden realizar grupos con posiciones discontinuas, es decir solo podrás formar tus grupos con aquellas posiciones que se encuentren de manera continua en horizontal y vertical, y contengan las cantidades aceptables (1, 2, 4, 8, etc.), en este caso la columna AB está vacía, lo que impide que se puedan agrupar los unos existentes.

Por lo tanto, en este ejemplo es posible hacer dos grupos con dos posiciones, los grupos fueron marcados con colores distintos para que se pueda notar que cada grupo va a corresponder a un elemento diferente dentro del resultado, la forma correcta de los grupos, puede verse en la figura 6:

Fig. 6.- Grupos correctos del mapa de la figura 4.

Dando como resultado:

Para obtener el resultado final debes poner atención en aquellas variables que no tienen ningún cambio dentro del grupo. Es importante que recuerdes que las variables que sufren cambio no son parte del resultado.

El resultado $\bar{B}C$ esta dado por los valores lógicos que le corresponden a la posición de cada variable en donde se encuentra el grupo, en este caso B tiene el valor 0 por lo que corresponde una negación y C tiene el valor 1 por lo que se mantiene como verdadera. Explicado de otra forma, si para cada uno de los unos que se encuentran en el grupo azul, colocamos las combinaciones de las variables en su representación binaria dentro de una tabla de verdad, se obtiene la tabla 1, en ella buscamos las variables que no cambian. En la tabla 1, es posible ver que en la columna correspondiente a la variable A, existe un cambio entre sus filas; en la columna correspondiente a la variable B, se mantiene el valor de 0; y en la columna que le corresponde a la variable C, se mantiene constante el valor de 1. Por lo que en la función resultante, A no forma parte de la ecuación, B es negado y C es no negado.

Tabla 1.- Comparación de las combinaciones de variables que forman el grupo $\bar{B}C$.

A	B	C
0	0	1
1	0	1

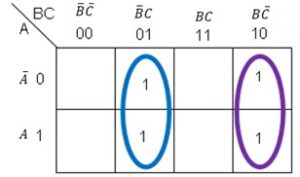
Para el resultado $B\bar{C}$, este lo podemos visualizar en la misma forma que el anterior, obteniendo la tabla 2, en donde es posible ver que en la columna correspondiente a la variable A, existe un cambio entre sus filas; en la columna correspondiente a la variable B, se mantiene el valor de 1; y en la columna que le corresponde a la variable C, se mantiene constante el valor de 0. Por lo que en la función resultante, A no forma parte de la ecuación, B es no negado y C es negado.

Tabla 2.- Comparación de las combinaciones de variables que forman el grupo $B\bar{C}$.

A	B	C
0	1	0
1	1	0

Ejemplo 2. Obtener la función booleana del mapa de Karnaugh de la figura 6:

Fig. 6.- Mapa de Karnaugh, ejemplo 2.

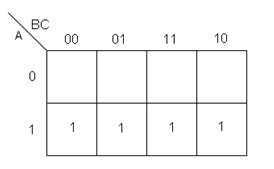
En este ejemplo es necesario recordar que se busca hacer grupos lo más grande posible, por lo que se tiene la posibilidad de un solo grupo de 4 posiciones, recordando también que el 4 es una potencia de 2, por lo que este grupo si está permitido.

El resultado correcto se muestra en la figura 7:

Fig. 7.- Resultado correcto del mapa mostrad en la figura 6.

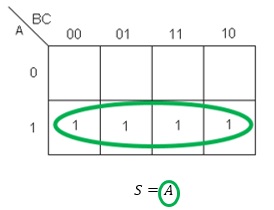
El resultado de este mapa es A, ya que como se mencionó anteriormente, esta es la única variable que no sufre cambios en sus valores lógicos dentro del grupo. Nuevamente podemos representar las posiciones de todos los unos que se encuentran dentro del grupo verde dentro de una tabla de verdad, tabla 3:

Tabla 3.- Comparación de las combinaciones de variables que forman el grupo $A$.

A	B	C
1	0	0
1	0	1
1	1	1
1	1	0

Podemos observar en la tabla de verdad que, dentro de la columna que representa a la variable B, existen cambios entre sus filas, hay valores 1 y valores 0; lo mismo sucede con la columna que representa a C, sin embargo, es posible observar que en la columna que representa a A, no existen cambios entre sus filas, permaneciendo constante el valor de 1, por lo que se mantienen como verdadera o no negada.

Ahora, si el grupo se hubiera posicionado en donde se encuentra la fila de A=0, entonces el resultado sería una negación, tal como se puede observar en la figura 8:

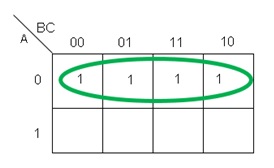Fig. 8.- Resultado inverso al grupo $A$ de la figura 6, dando como resultado $S=\bar{A}$ .

Un resultado erróneo de este ejemplo, sería el mostrado en la figura 9, en la que se pueden observar dos grupos, si bien es cierto que estos grupos son correctos, también es necesario recordar que una de las reglas dice que se deben de realizar grupos lo más grande posibles, dos grupos de 2 elementos son más pequeños que un grupo de 4 elementos. El resultado de los grupos del mapa de la figura 9 sería $S=A\bar{B}+A\bar{B}$, que es una función más compleja que $A$, que es el resultado correcto.

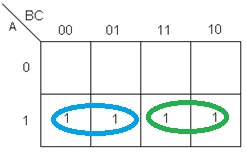Fig. 9.- Resultado erróneo del mapa mostrado en la figura 6, se forman dos grupos en lugar de uno sólo.

Ejemplo 3. Obtener la función booleana del mapa de Karnaugh de la figura 10:

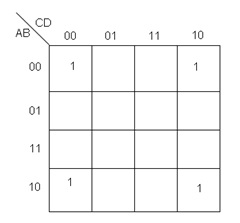Fig. 10.- Tercer ejemplo de mapa de Karnaugh.

La particularidad de este ejemplo es que con él se puede mostrar la unión de las celdas de las esquinas. En este caso, es posible realizar un solo grupo, un grupo en el que se junten las 4 esquinas, tal como lo podemos observar en la figura 11:

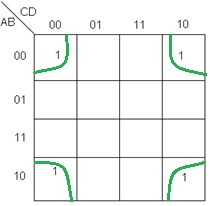Fig. 11.- Resolución del mapa de la figura 10, en donde se agrupan las 4 esquinas del mismo.

La agrupación de la figura 11, da como resultado la siguiente función:

$$S=\bar{B}\bar{D}$$

De igual forma que en ejemplos anteriores, vamos a convertir las posiciones de cada uno de los unos que compoenen el grupo verde a su representación en tabla de verdad para poder explicar el resultado obtenido. La tabla de verdad que representa cada una de las 4 posiciones agrupadas, se muestra a continuación:

Tabla 4.- Comparación de las combinaciones de variables que forman el grupo $S=\bar{B}\bar{C}$.

A	B	C	D
0	0	0	0
0	0	1	0
1	0	0	0
1	0	1	0

Como es posible ver en la tabla, las columnas que representan a A y a C, tienen cambios de valores entre sus filas, sin embargo, la columna que representa a B permanece con valores constantes iguales a 0 y la columna que representa a D también permanece con valores constantes iguales a 0, por lo que las variables A y C no forman parte de la función, mientras B y D permanecen como variables negadas.

Ejemplo 4. Obtener la función booleana del mapa de Karnaugh de la figura 12:

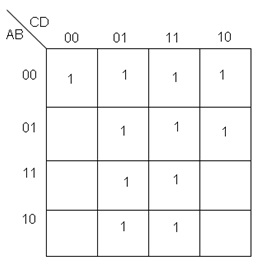Fig. 12.- Mapa de Karnaught, ejemplo 4.

Para resolver este ejemplo y encontrar la solución más reducida, es indispensable recordar dos de las reglas de solución, estas son: los grupos deben ser lo más grande posibles y que sean formados por una cantidad de unos que represente un conjunto de $2^{n}$ elementos, y los grupos pueden empalmarse siempre y cuando exista al menos un 1 sin agrupar. Una vez recordado esto la solución se muestra n la figura 13.

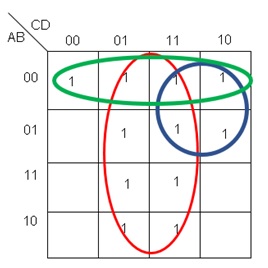Fig.13.- Resolución del mapa de Karnaugh de la figura 12.

Los grupos generados en la figura 12, dan como resultado la siguiente función, indicando en cada elemento de la función el color del grupo al que pertenece:

Un error común que se puede presentar en la resolución del mapa de la figura 12, es el mostrado en la figura 14, en ella se puede ver un grupo encerrado en rosa, este grupo es redundante, ya que agrupa unos que ya fueron agrupados previamente por los círculos rojo y morado.

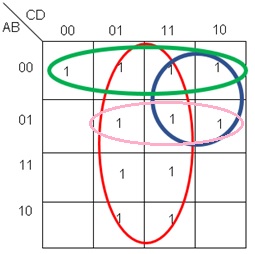Fig. 14.- Adición de un grupo redundante.

Ejemplo 5. Obtener la función booleana del mapa de Karnaugh de la figura 15:

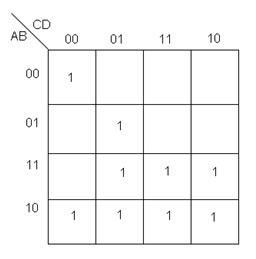Fig. 15.- Mapa de Karnaugh, ejemplo 5.

Para este mapa podemos tener la solución incorrecta mostrada en la figura 16:

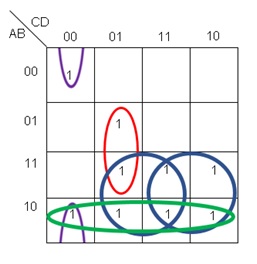Fig. 16.- Resolución incorrecta del mapa de la figura 15.

EL mapa de la figura 16 presenta una agrupación incorrecta ya que se puede ver que el grupo encerrado en verde, es un grupo redundante, por lo cual no es apropiado. Esta agrupación da como resultado la siguiente función, la cual se ha reducido:

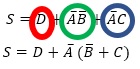
$$S=A\bar{B}+AD+AC+B\bar{C}D+\bar{B}\bar{C}\bar{D}$$

$$S=A(\bar{B}+D+C)+ \bar{C}(BD+\bar{B}\bar{D})$$

$$S= A(\bar{B}+D+C)+ \bar{C}(B \bigodot D)$$

La forma correcta de agrupar el mapa de la figura 15, es la mostrada en la figura 17.

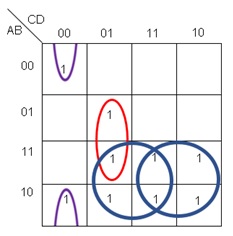Fig. 17.- Forma correcta de agrupación.

La función resultante de la figura 16, se muestra a continuación.

$$S=AD+AC+B \bar{C} D+\bar{B} \bar{C}\bar{D}$$

$$S=A(D+C)+ \bar{C}(BD+\bar{B}\bar{D})$$

$$S= A(D+C)+ \bar{C}(B \bigodot D)$$

Para la resolución de mapas de Karnaugh en línea, se puede visitar la siguiente página de internet:

http://www.32×8.com/index.html