Álgebra Booleana
El álgebra de Boole es una herramienta diseñada para poder representar proposiciones lógicas en forma algebraica. Desarrollada originalmente en 1847 por George Boole.
Actualmente, esta álgebra es utilizada ampliamente en el diseño y simplificación de sistemas digitales binarios, es decir, sistemas que basan todo su comportamiento en los valores $\{0, 1\}$.
El álgebra de Boole ha sido de gran utilidad para poder generar circuitos lógicos eficientes y simplificados en su mínima expresión, ¿Qué significa esto?
Un circuito digital está compuesto por un conjunto de entradas con valores binarios, las combinaciones que se pueden formar por medio de estas entradas determinarán el comportamiento que se tendrá en la o las salidas del sistema, es decir, tenemos un conjunto de actuadores de salida dependientes del comportamiento de las variables de entrada. Dependiendo del número de variables de entrada, se tiene el número de combinaciones que se pueden generar por medio de $NC=2^{n}$, dónde $n$ es el número de entradas, sin embargo, el número de salidas puede ser definido sin ninguna restricción.
Las combinaciones mencionadas pueden ser representadas por medio de funciones lógicas o algebraicas, por ejemplo, la combinación de entrada $0101$ puede ser representada por medio de la función $\overline{A}B\overline{C}D$, donde la barra por encima de una variable indica que tiene un valor negado o 0. La suma de estas combinaciones genera ecuaciones lógicas extensas que tienen el mismo comportamiento lógico que una expresión más pequeña, por ejemplo la siguiente suma de funciones:
$$S=\overline{A}\overline{B}CD+\overline{A}BC+C\cdots\cdots (1)$$
Tiene el mismo comportamiento lógico que la función
$$S=\overline{A}C (2)\cdots\cdots$$
Es fácil notar, que la segunda función es mucho más simple que la primera. Esta simplificación se logra aplicando los axiomas lógicos booleanos a la primera de las funciones presentadas.
La realización de la simplificación en una función lógica no sólo impacta en la función matemáticas, sino que impacta en el gasto realizado en espacio y monetario, ya que entre más elementos tenga una función lógica, en el momento de construir un circuito lógico, se tendrán más componentes, utilizando mayor espacio en su construcción, y obviamente, invirtiendo mayor cantidad monetaria en la adquisición e instalación de los mismos.
Existen 3 compuertas lógicas básicas, sobre las cuales cae el diseño de cualquier circuito lógico, la compuerta AND, OR y NOT. Cada operación que se marca sobre una función booleana, corresponde a una compuerta; A la compuerta OR, le corresponde la suma; A la compuerta AND, le corresponde la multiplicación; A la compuerta NOT, le corresponde la negación. Si contamos el número de sumas, multiplicaciones y negaciones que contiene una función, se puede saber la cantidad de compuertas necesarias para implementar tal función. Por ejemplo, la función (1) requiere 2 compuertas OR, 6 compuertas AND y 4 compuertas NOT (Considerando compuertas lógicas de dos entradas), mientras que la función (2) requiere solamente una compuerta AND y una compuerta NOT.
Debido a que, para la realización de las funciones lógicas podemos utilizar las combinaciones de variables que den como resultado 1, o las combinaciones que den como resultado 0, las funciones booleanas se pueden expresar como suma de productos o producto de sumas, respectivamente. Una suma de productos esta definida en la forma $ S= \overline{A}BC+A\overline{B}\overline{C}+AB\overline{C}$, mientras que un producto de sumas está definido por $ S= (\overline{A}+B+C)(A+\overline{B}+\overline{C})(A+B+\overline{C})$.
Teoremas del álgebra Booleana
Para minimizar las diferentes funciones booleanas, es necesario utilizar los teoremas lógicos de Boole. Los teoremas de Boole son siempre verdaderos, es decir, son axiomas que no necesitan prueba, se enlistan en pares porque cada ley válida tiene una dualidad entre 0 y 1 y/o + y ⋅. Con estos teoremas facilitamos el análisis y obtenemos una reducción de los circuitos digitales.
En la tabla 1, se muestra una lista con cada uno de los teoremas y su dual, es necesario mencionar que a cada teorema se le esta representando con una figura y color, es to se hace con la intención de indicar cuando se ha usado cada teorema en la resolución de funciones que se tendrán más adelante.
Tabla1. Funciones y su figura identificadora.
A continuación, se muestra algunos ejemplos en el que se podrá apreciar la utilidad de los teoremas antes mencionados y como se aplican.
NOTA: A partir de aquí, cada uno de los teoremas mostrados en la tabla 1 que se utilizan en cada uno de los ejemplos, es marcado por una figura y color diferente para que sea más fácil poder ubicar que teorema se utilizó en cada ejemplo.
Ejemplo 1. Reducir la siguiente función booleana a su mínima expresión, utilizando los teoremas lógicos antes presentados.
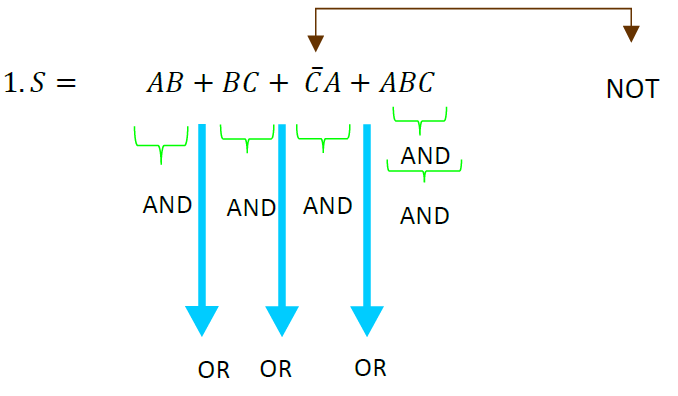
En este ejemplo, como se puede observar en la función, se necesitan 5 compuertas AND, 3 compuertas OR y 1 compuerta NOT, se utilizarán los teoremas del algebra de Boole para simplificar esa función y posteriormente poder armar el circuito.
Factorización de elementos, en este primer paso se buscan variables que compartan más de una sección de la función, y posteriormente factorizar tal variable, en este caso $A$, obteniendo:
$$S=A(B+BC+\overline{C})+BC$$
Segunda factorización de elementos. Dentro del paréntesis, se encuentra la variable $B$, que es común en cada sección, por lo que podemos factorizarla también.
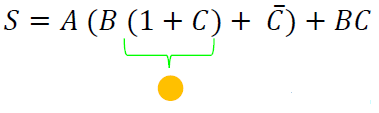
Podemos notar que se utiliza el segundo teorema en su primera dualidad.
$$A+1=1$$
Aplicando el teorema, resulta:
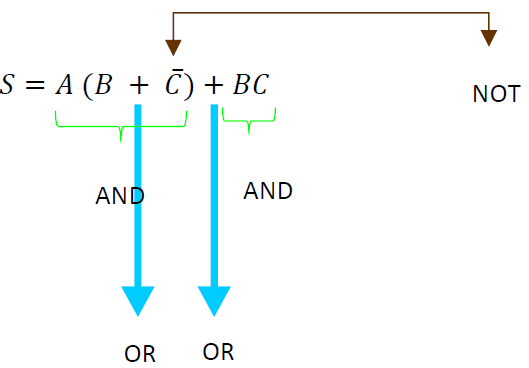
Con esto podemos observar que la cantidad de compuertas lógicas se ha reducido de 5 a 2 AND, de 3 a 2 OR y la NOT permanece.
A continuación, en la figura 1 se muestra el diagrama esquemático del resultado de la reducción de la función original.
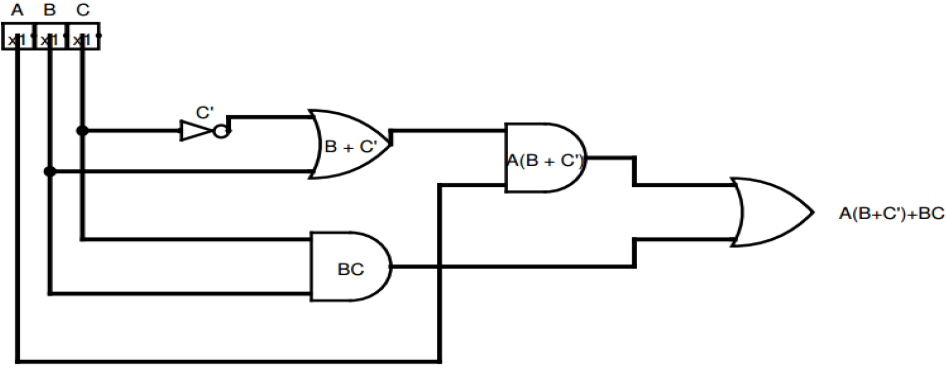
Fig. 1.- Diagrama esquemático de la función $S=A(B+\overline{C})+BC$.
Ejemplo 2. Utilizando álgebra booleana, simplifica la siguiente función lógica.
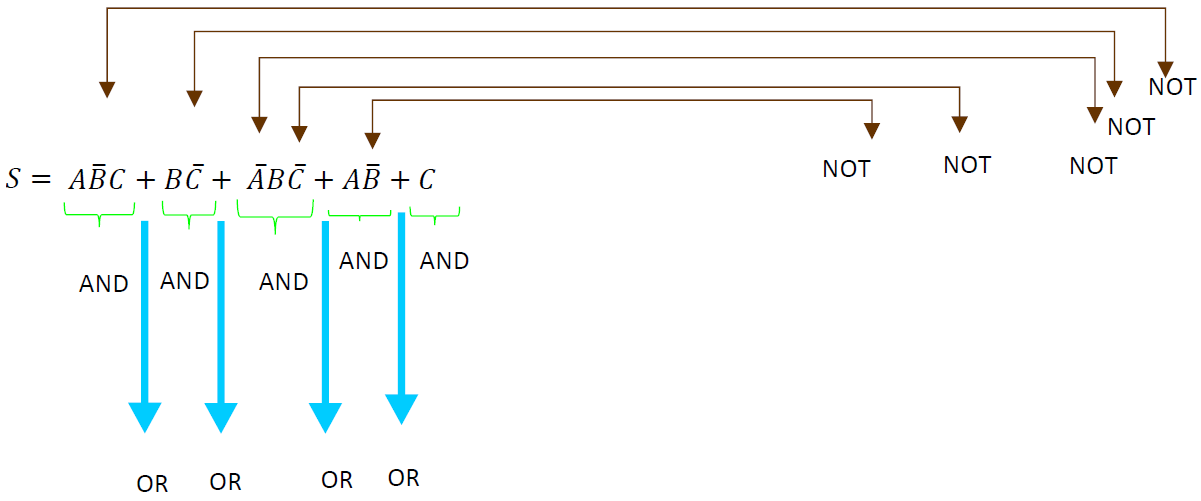
En este ejemplo, como vemos en la función a resolver, se tienen 5 compuertas AND, 4 compuertas OR y 5 compuerta NOT, se utilizarán los teoremas del algebra de Boole para simplificar esa función y posteriormente poder armar el circuito.
Factorización de elementos. En este primer paso se buscan variables que compartan más de una sección de la función, y posteriormente factorizar tal variable, en este caso $C$, obteniendo:
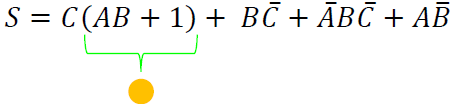
Vemos que dentro del paréntesis se puede aplicar el teorema 2 de la tabla1, aplicando el teorema, resulta:
$$S=C+B\overline{C}+\overline{A}B\overline{C}+A\overline{B}$$
Segunda factorización de elementos. Nuevamente, es posible factorizar la variable $B$, teniendo:
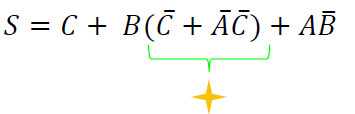
Aplicando el teorema, resulta:
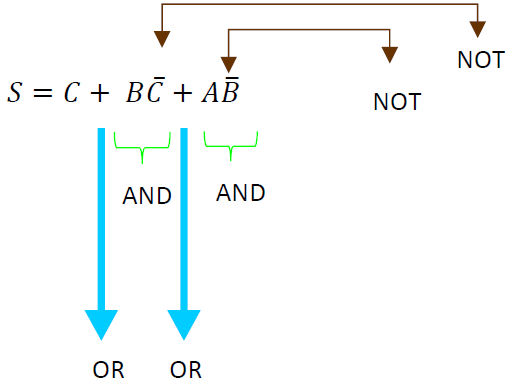
Con esto podemos observar que la cantidad de compuertas lógicas se ha reducido de 5 a 2 AND, de 4 a 2 OR y de 5 a 2 NOT.
Ejemplo 3. Determina la expresión mínima de la siguiente función lógica.
En este tercer ejemplo se mostrará como una función puede tener diferentes soluciones, sin embargo, hay que recordar que aunque visualmente sean diferentes, lógicamente representan el mismo comportamiento.
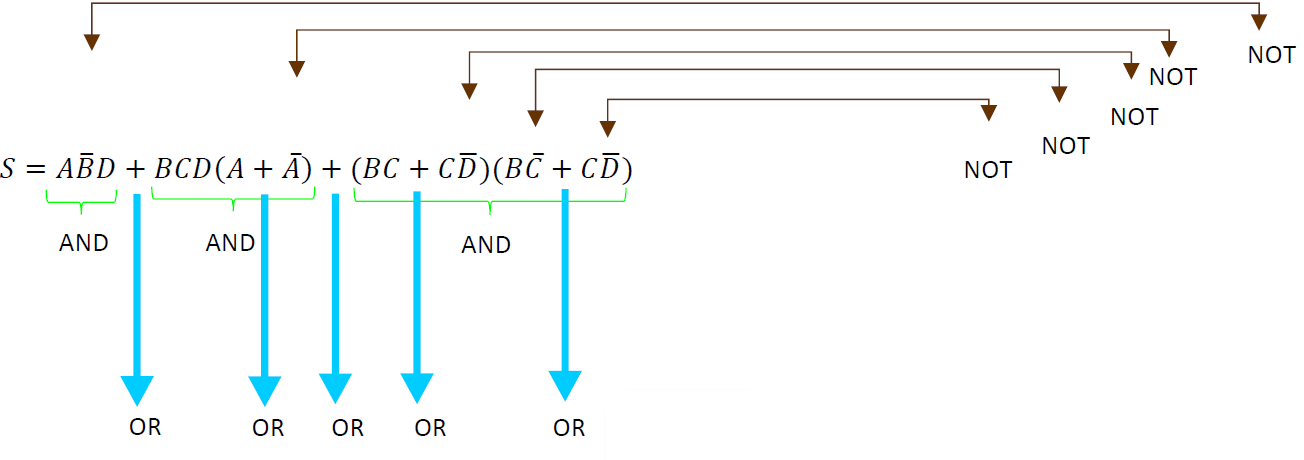
En este ejemplo se tienen 3 compuertas AND, 5 compuertas OR y 5 compuerta NOT, se utilizarán los teoremas del algebra de Boole para simplificar esa función y posteriormente poder armar el circuito.
Realización de las primeras operaciones para quitar los paréntesis, es decir, se realizan las multiplicaciones correspondientes, obteniendo:
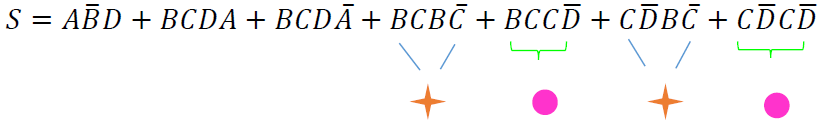
Aplicando los teoremas marcados, resulta:
$$S=A\overline{B}D+BCDA+BCD\overline{A}+0+BC\overline{D}+0+C\overline{D}$$
Factorizando elementos $BC$, y posteriormente $D$:
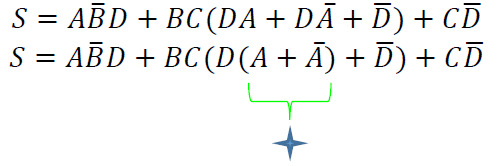
Aplicando el teorema, resulta:
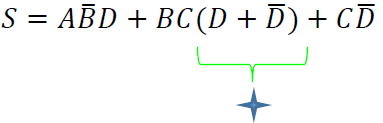
Aplicando una última factorización en la variable C.
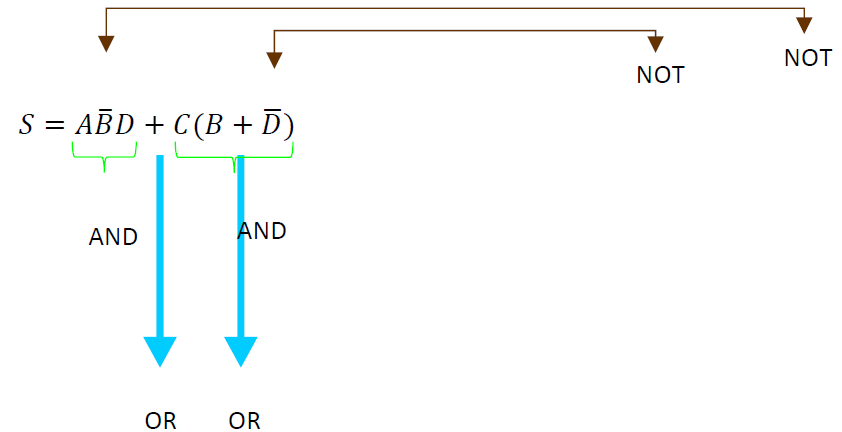
Con esto podemos observar que la cantidad de compuertas lógicas se ha reducido de 3 a 2 AND, de 5 a 2 OR y de 5 a 2 NOT permanece.
Segunda opción de solución.
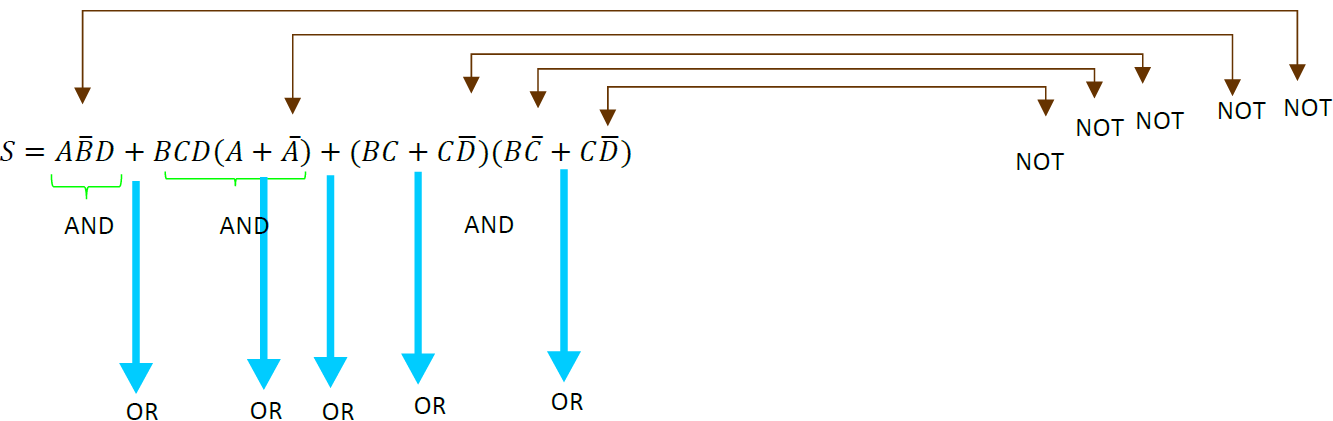
En este ejemplo se necesitan 3 compuertas AND, 5 compuertas OR y 5 compuerta NOT, se utilizarán los teoremas del algebra de Boole para simplificar esa función y posteriormente poder armar el circuito.
Realización de las primeras operaciones para quitar los paréntesis.
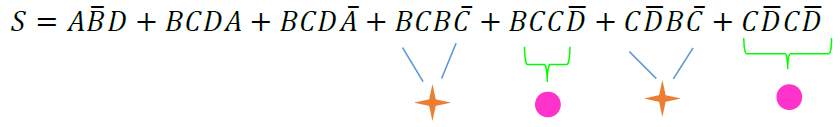
Aplicando el teorema, resulta:
$$S=A\overline{B}D+BCDA+BCD\overline{A}+0+BC\overline{D}+0+C\overline{D}$$
Factorizando elementos
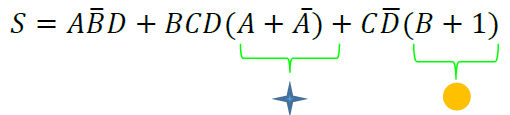
Ultima factorización posible
Con esto podemos observar que la cantidad de compuertas lógicas se ha reducido de 3 a 2 AND, de 5 a 2 OR y de 5 a 2 NOT permanece.
La simplificación ahora es un poco más corta pero el resultado es el mismo. Que en la anterior.
Tercera forma de solución
Ahora se mostrará una manera más de solucionar la misma función.
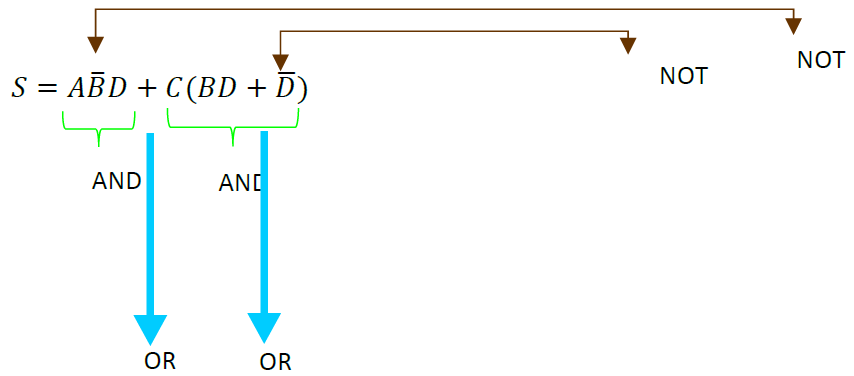
En este ejemplo se necesitan 3 compuertas AND, 5 compuertas OR y 5 compuerta NOT, se utilizarán los teoremas del algebra de Boole para simplificar esa función y posteriormente poder armar el circuito.
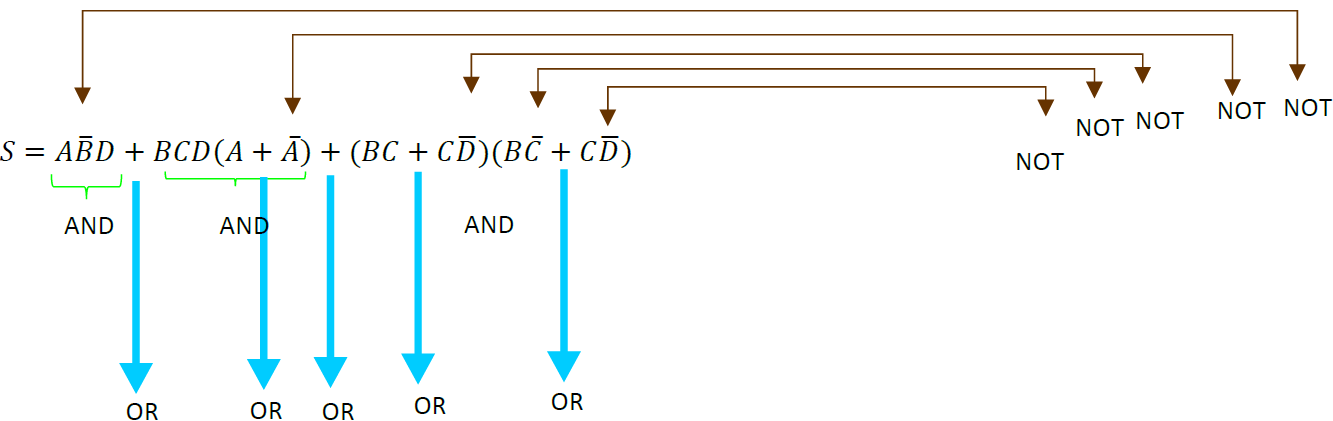
Realización de las primeras operaciones para quitar los paréntesis.
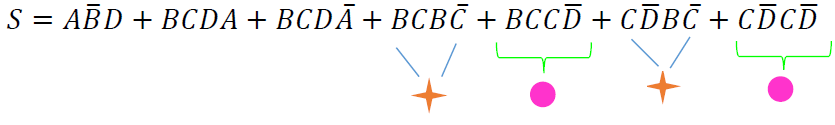
Aplicando el teorema, resulta:
$$S=A\overline{B}D+BCDA+BCD\overline{A}+0+BC\overline{D}+0+C\overline{D}$$
Factorizando elementos.
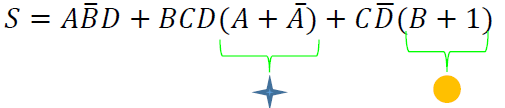
Ultima factorización posible
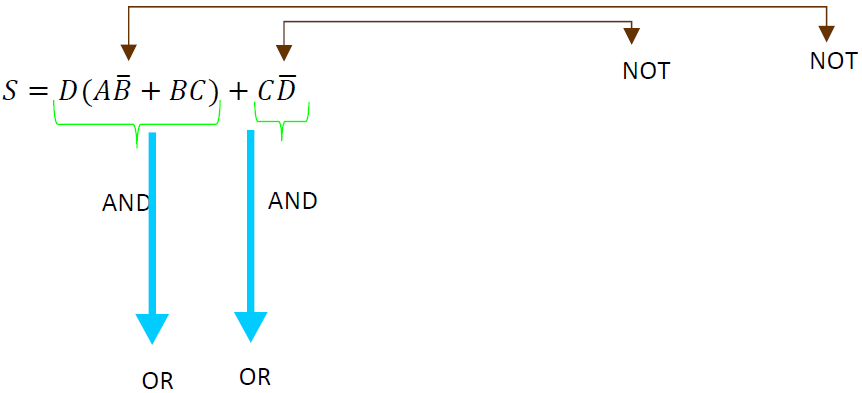
Con esto podemos observar que la cantidad de compuertas lógicas se ha reducido de 3 a 2 AND, de 5 a 2 OR y de 5 a 2 NOT permanece.
En esta simplificación vemos que el resultado es diferente, pero la evaluación lógica es correcta, hay que observar, que etas variaciones se an principalmente por las variables que se van factorizando en cada paso, esta situación se repite mucho en este tipo de funciones, es decir, existen varias variables que pueden ser factorizadas, y el lector puede decidir factorizar la que más le convenga.
Podemos obtener las tablas de verdad de los resultados obtenidos en cada uno de los casos calculados en la página https://www.dcode.fr/boolean-truth-table y de esta forma verificar su igualdad lógica.


