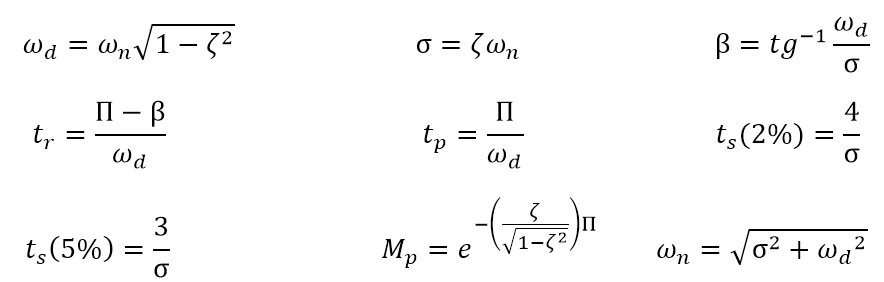Sistemas de segundo orden

 

Todo sistema de segundo orden está representado por la expresión general:

$$
\begin{equation}
a_{2}\frac{d^{2}y}{dt}+a_{1}\frac{dy}{dt}+a_{0}y=b_{0}U(t)
\end{equation}
$$

Que también puede describirse como

$$
\begin{equation}
\tau^{2}\frac{d^{2}y}{dt}+2\zeta\tau\frac{dy}{dt}+y=kU(t)
\end{equation}
$$

Donde:

$$\tau^{2}=\sqrt{\frac{a_{2}}{a_{0}}}$$

$$2\zeta\tau=\frac{a_{1}}{a_{0}}$$

$$k=\frac{b_{0}}{a_{0}}$$

Sacando la transformada de Laplace (Formulario) de (2), considerando condiciones iniciales igual a cero, tenemos:

$$
\begin{equation}
\tau^{2}S^{2}Y(S)+2\zeta\tau SY(S)+Y(S)=KU(S)
\end{equation}
$$

Despejando $Y(S)$ de (3), tenemos:

$$
\begin{equation}
Y(S)\left ( \tau^{2}S^{2}+2\zeta\tau S+1\right )=KU(S)
\end{equation}
$$

Y obteniendo la función de transferencia de (4), tenemos:

$$
\begin{equation}
\frac{Y(S)}{U(S)}=\frac{K}{\tau^{2}S^{2}+2\zeta\tau S+1}
\end{equation}
$$

Normalizando (5), todo entre $\tau^{2}$

$$
\begin{equation}
\frac{Y(S)}{U(S)}= \frac{K\frac{1}{\tau^{2}}}{\frac{\tau^{2}S^{2}}{\tau^{2}}+\frac{2\zeta\tau S}{\tau^{2}}+\frac{1}{\tau^{2}}}= K\left(\frac{\frac{1}{\tau^{2}}}{S^{2}+\frac{2\zeta S}{\tau}+\frac{1}{\tau^{2}}}\right)
\end{equation}
$$

Si tenemos que:

$$\tau^{2}=\frac{1}{\omega_{n}^{2}}$$

$$\tau=\frac{1}{\omega_{n}}$$

Donde $\omega_{n}$  es la frecuencia natural del sistema, $\tau$ es el periodo natural del sistema y ζ es el factor de amortiguamiento.

Podemos sustituir estas igualdades en (6), quedando:

$$
\begin{equation}
\frac{Y(S)}{U(S)}=K\frac{\omega_{n}^{2}}{S^{2}+2\zeta\omega_{n}S+\omega_{n}^{2}}
\end{equation}
$$

Lo interesante de estos sistemas, es que el comportamiento en tiempo y respuesta de cualquier sistema está dado por K, ζ y ω_n .

La ecuación (7) es la representación general de un sistema de segundo orden, y a partir de su denominador podemos obtener sus raíces, que están dadas por:

$$r_{1,2}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}= \frac{-2\zeta\omega_{n}\pm \sqrt{4(\zeta\omega_{n}) ^{2}-4\omega_{n}^{2}}}{2(1)}$$

$$r_{1,2}= \frac{-2\zeta\omega_{n}\pm \sqrt{4[(\zeta\omega_{n}) ^{2}-\omega_{n}^{2}]}}{2(1)}=\frac{-2\zeta\omega_{n}\pm 2\sqrt{(\zeta\omega_{n}) ^{2}-\omega_{n}^{2}}}{2(1)}$$

$$
\begin{equation}
r_{1,2}=-\zeta\omega_{n}\pm \sqrt{(\zeta\omega_{n}) ^{2}-\omega_{n}^{2}}
\end{equation}
$$

Podemos ver de (8) que las raíces dependen completamente de ζ. A partir de esta observación, podemos distinguir 4 casos:

0 < ζ <1	Subamortiguado	2 Polos complejos conjugados
ζ = 1	Críticamente amortiguado	2 Polos reales iguales
ζ > 1	Sobreamortiguado	2 Polos reales distintos
ζ = 0	No amortiguado	2 Polos imaginarios puros

Estos 4 comportamientos dependen de las posiciones de los polos de la función, estos pueden ser representados de acuerdo a las siguientes figuras:

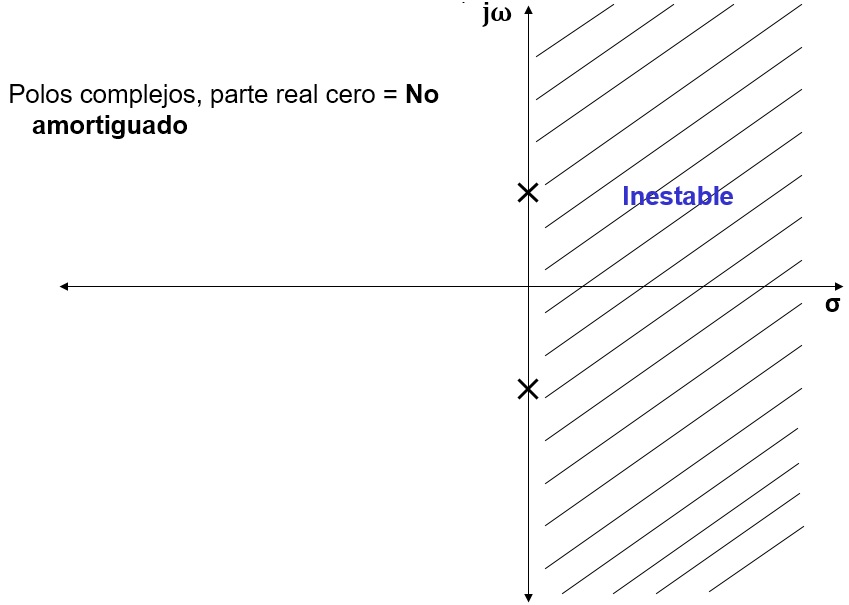
Fig.1.- Representación de los polos de una función en un sistema No amortiguado.

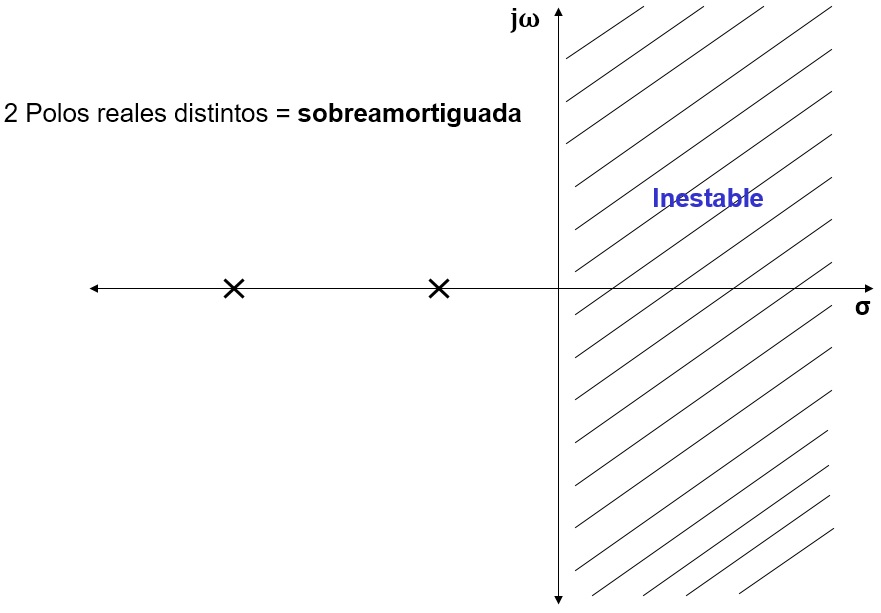
Fig. 2.-Representación de los polos de una función en un sistema sobreamortiguado,

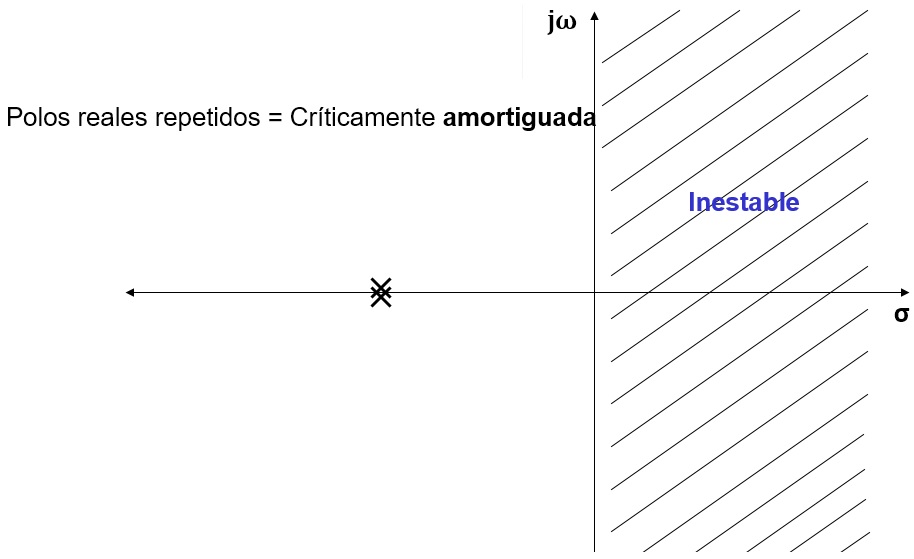
Fig. 3.-Representación de los polos de una función en un sistema críticamente amortiguado,

Fig. 4.-Representación de los polos de una función en un sistema subamortiguado.

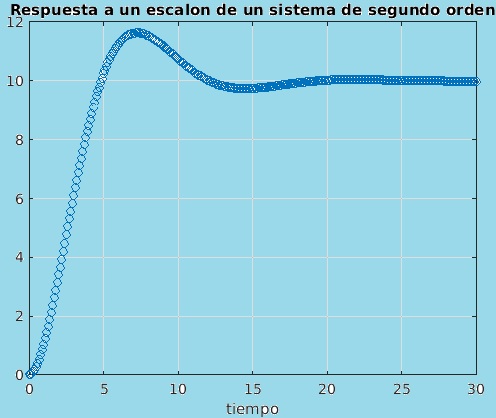
Un sistema de segundo orden tiene el comportamiento  general, en sus salida, mostrado en la figura 5.

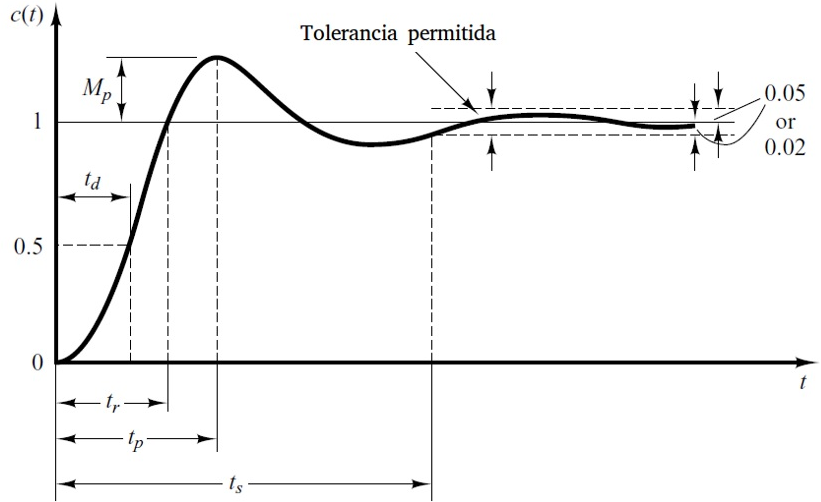
Fig.5.- Comportamiento de la señal de salida de un sistema de segundo orden, comportamiento que corresponde a una señal escalón en la entrada, donde: $M_{p}$ es el valor del  máximo pico alcanzado, $t_{d}$ es el tiempo que tarda la señal al llegar al 50% del valor deseado, $t_{r}$ es el tiempo necesario en el que se pasa de 0% al 100% del valor deseado de la señal por primera vez, $t_{p}$ es el tiempo que tarda la señal en llegar al pico máximo, $t_{s}$ es el tiempo que tarda la señal en estabilizarse. Se tiene una tolerancia de estabilización del 2% al 5% de error con respecto al valor deseado o esperado.

Podemos notar en la figura 5, que la señal de salida se compone de diferentes elementos, estos elementos son los que definen su comportamiento. A partir de la ecuación (7), es posible determinar el comportamiento de la señal de salida de un sistema de segundo orden, calculando los elementos que la componen, utilizando las siguientes ecuaciones:

Para graficar en Matlab la señal mostrada en la cabecera de esta página, se debe de utilizar el siguiente script: