Sistema de primer orden.
Fig. 1.- Circuito capacitivo, inductivo y resistivo. Figura recuperada de https://pixabay.com/es/photos/circuito-placa-de-circuito-resistor-1443251/ .
El orden de un sistema se representa por medio del polinomio que se encuentra en el denominador de la ecuación que representa su función de transferencia. Como es bien sabido, este polinomio define el número de polos con los que el sistema trabaja. Los sistemas de primer orden se pueden analizar a partir de la respuesta temporal a cierto tipo de entradas, tales como el escalón, la rampa y el impulso unitario.
La ecuación característica de los sistemas de primer orden se muestra a continuación:
$$a\frac{dy(t)}{dt}+by(t)=cx(t)\cdots \cdots (1)$$
Donde a, b y c son los coeficientes del polinomio
A esta ecuación le aplicamos la transformada de Laplace para simplificarla y así poder obtener la función de transferencia $\Delta=\frac{y(s)}{x(s)}$
Aplicando la transformada de Laplace a 1, tenemos:
$$(as+b)y(s)=cx(s) \cdots \cdots (2)$$
Despejando $y(s)$ y $x(s)$ tal que $\frac{y(s)}{x(s)}$
$$\Delta=\frac{y(s)}{x(s)}=\frac{c}{as+b}\cdots \cdots (3)$$
Dividiendo todos los elementos de 3 entre b, tenemos:
$$\Delta=\frac{\frac{c}{b}}{\frac{a}{b}s+1}\cdots \cdots (4)$$
Dónde $\frac{c}{b}=K$ y $\frac{a}{b}=T$.
De lo que podemos determinar la función de trasferencia:
$$\Delta\frac{y(s)}{x(s)}=\frac{K}{Ts+1}\cdots \cdots (5)$$
Dónde:
$K$=Ganancia del sistema de primer orden.
$T$= Constante de tiempo del sistema de primer orden.
Ahora, para analizar su comportamiento, vamos a someter el sistema de la ecuación 5 a las entradas antes mencionadas
Respuesta a una entrada tipo escalón unitario.
Sabemos que la transformada de Laplace de la función escalón unitario es $\frac{1}{s}$, por lo tanto $x(s)=frac{1}{s}$:
$$\frac{y(s)}{x(s)}=\frac{1}{Ts+1}$$
Tenemos que la salida del sistema esta definido por
$$y(s)=\frac{1}{Ts+1}\left ( \frac{1}{s} \right )=\frac{1}{s(Ts+1)}\cdots \cdots (6)$$
La ecuación 6, la podemos resolver por medio del método de fracciones parciales simples, lo que nos da la siguiente expresión:
$$y(s)=\frac{1}{s(Ts+1)}=\frac{A}{s}+\frac{B}{(Ts+1)}\cdots \cdots (7)$$
Obteniendo los valores correspondientes a A y a B, tenemos:
$$A=\left |s\frac{1}{s(Ts+1)}\right|_{s=0}=1$$
$$B=\left | (Ts+1)\frac{1}{s(Ts+1)} \right |_{s=\frac{-1}{T}}=-T$$
Sustituyendo A y B en (7):
$$y(s)=\frac{1}{s}-\frac{T}{Ts+1}\cdots\cdots(8)$$
Ya teniendo las fracciones definidas, podemos aplicar la transformada inversa de Laplace a (8):
$$y(t)=1-\mathcal{L}^{-1}\left \{ \frac{T}{Ts+1} \right \}\cdots\cdots(9)$$
Normalizando la parte $\frac{T}{Ts+1}$, de (9), es decir dividiendo todo entre $T$, para dejar el elemento lineal $s$ con un coeficiente igual a 1:
$$\frac{\frac{T}{T}}{\frac{Ts}{T}+\frac{1}{T}}=\frac{1}{s+\frac{1}{T}}$$
Tenemos
$$y(t)=1-\mathcal{L}^{-1}\left \{ \frac{1}{s+\frac{1}{T}} \right \}$$
Lo cual, aplicando la $ \mathcal{L}^{-1}$, da como resultado:
$$y(t)=1-e^{\frac{-t}{T}}\cdots\cdots(10)$$
L ecuación (10), es la ecuación en función del tiempo que representa a nuestro sistema con una entrada tipo escalón, ahora bien, si suponemos que $t=T$ , obtenemos que:
$$y(t)=1-e^{\frac{-t}{T}}=1-e^{1}=0.632$$
Tenemos que el valor $y(t)=0.632$, es una constante que indica el momento en el que la respuesta alcanzó 63.2% de su cambio total.
La respuesta en el tiempo del sistema de primer orden, la podemos observar en la figura 2. Vemos que en la salida existe un retraso para llegar al valor deseado, en este caso tarda un tiempo 3T para alcanzar el 95% del valor deseado.
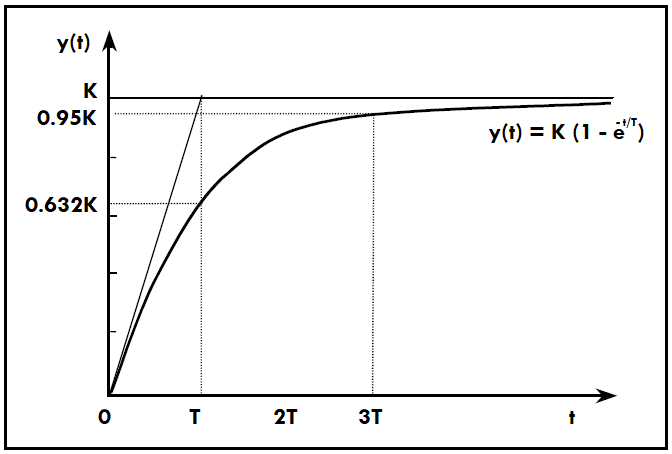
Fig. 2.- Curva de respuesta de un sistema de primer orden a una entrada escalón.
Para obtener la respuesta de un sistema de primer orden a una entrada escalón por medio de Matlab, podemos utilizar el siguiente código:
|
1 2 3 4 5 6 7 8 9 10 |
K=1; tau=1; num=K; den=[tau 1]; t=[0:0.1:10]; salida=step(num,den,t); plot(t,salida) title('Respuesta a un escalón unitario'); xlabel('tiempo'); grid; |
Respuesta a la rampa unitaria.
Nuevamente, teniendo como punto de partida la ecuación (5),
$$\frac{y(s)}{x(s)}=\frac{1}{Ts+1}$$
Tenemos que la transformada de Laplace de la función rampa unitaria es $\frac{1}{s^{2}}$ vamos a someter a nuestro sistema a esta entrada, es decir:
$$y(s)=\frac{1}{Ts+1}\left ( \frac{1}{s^{2}} \right )=\frac{1}{s^{2}(Ts+1)}\cdots\cdots(11)$$
La ecuación (11) puede ser resuelta por medio de fracciones parciales, considerando 3 raíces o polos, quedando en la forma:
$$y(s)=\frac{1}{s^{2}(Ts+1)}=\frac{A}{s}+\frac{B}{S^{2}}+\frac{C}{(Ts+1)}\cdots\cdots(12)$$
Obteniendo los valores de A, B y C, tenemos:
$$B=\left | s^{2}\frac{1}{s^{2}(Ts+1)} \right |_{s=0}=1$$
$$C=\left | (Ts+1)\frac{1}{s^{2}(Ts+1)} \right |_{s=\frac{-1}{T}}=T^{2}$$
Como tenemos dos raíces, A y B, con el mismo valor, calculamos el valor de A en la siguiente forma. Pariendo de la ecuación (12), tenemos que:
$$\frac{1}{s^{2}(Ts+1)}=\frac{A}{s}+\frac{B}{s^{2}}+\frac{C}{(Ts+1)}$$
Multiplicamos el lado derecho de (12) por el denominador del lado izquierdo:
$$1=\left ( \frac{A}{s}+\frac{B}{s^{2}}+\frac{C}{(Ts+1)}\right )[s^{2}(Ts+1)]$$
Realizando la multiplicación por cada elemento del lado derecho, obtenemos:
$$1=As(Ts+1)+B(Ts+1)+Cs^{2}\cdots\cdots(13)$$
Sustituyendo los valores de B y C en (13):
$$1=As(Ts+1)+1(Ts+1)+T^{2}s^{2}\cdots\cdots(14)$$
Suponiendo que $s=1$, tenemos:
$$1=A(T+1)+T+1+T^{2}\cdots\cdots(15)$$
Despejando A de (15):
$$A=\frac{1-T-1-T^{2}}{T+1}=\frac{-T-T^{2}}{T+1}=-T\frac{T+1}{T+1}=-T$$
Ya habiendo obtenido los tres valores de A, B y C, estos los sustituimos en la ecuación (12), dando como resultado:
$$y(s)=\frac{-T}{s}+\frac{1}{s^{2}}+\frac{T^{2}}{(Ts+1)}\cdots\cdots(16)$$
Aplicando la transformada inversa de Laplace a (16):
$$y(t)=-T+t+\mathcal{L}^{-1}\left \{ \frac{T^{2}}{(Ts+1)} \right \}$$
Para poder aplicar la $\mathcal{L}$ a $\frac{T^{2}}{(Ts+1)} $ es necesario normalizar esa parte para dejar el elemento lineal con un coeficiente igual a 1, dividimos tal sección entre $T$:
$$\frac{T^{2}}{(Ts+1)}=\frac{\frac{T^{2}}{T}}{\frac{Ts}{T}+\frac{1}{T}}=\frac{T}{s+\frac{1}{T}}$$
Quedando:
$$y(t)=-T+t+T\mathcal{L}^{-1}\left \{ \frac{1}{s+\frac{1}{T}} \right \}\cdots\cdots(17)$$
Con esta representación, ahora si es posible aplicar la $\mathcal{L}^{-1}$a (17), de lo cual obtenemos:
$$y(t)=-T+t+Te^{\frac{-t}{T}}\cdots\cdots(18)$$
La ecuación (18) es la representación general de nuestro sistema de primer orden cuando se le ingresa como entrada una señal rampa, obteniendo la salida $y(t)$.
Sin embargo, para realizar la comparativa con respecto al valor de entrada $y(r)$, es necesario calcular el error existente en $y(t)$ , en la siguiente forma:
$$e=y(r)-y(t)$$
Donde:
$y(r)$ es una señal rampa pura.
$y(t)$ es la señal de salida después de ser procesada por nuestro sistema.
Ahora bien, suponiendo $y(r)=t$ :
$$e=t-\left ( -T+t+Te^{\frac{-t}{T}} \right )=t+T-t-Te^{\frac{-t}{T}}$$
$$e=T\left ( 1-e^{\frac{-t}{T}} \right )\cdots\cdots(19)$$
De la ecuación (19) se puede observar que conforme $t$ tiende a infinito, $e^{\frac{-t}{T}}$ se aproxima a cero, por tanto, la señal de error $e$ se aproxima a $T$.
En la figura 3, podemos observar el comportamiento de un sistema de primer orden, comparando una entrada rampa con respecto a la salida , se puede observar el error en la salida.
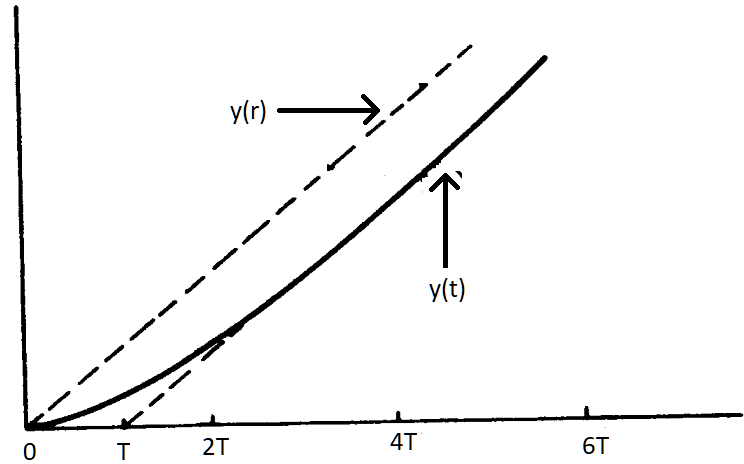
Fig. 3.- Curva de respuesta de un sistema de primer orden a una entrada rampa.
Para graficar una señal de salida de un sistema de primer orden cuando se tiene una señal de entrada rampa, se puede utilizar el siguiente código de Matlab:
|
1 2 3 4 5 6 7 8 9 10 11 |
K=1; tau=1; num=K; den=[tau 1]; t=[0:0.1:10]; rampa=t; salida=lsim(num,den,rampa,t); plot(t,salida,t,rampa); title('Respuesta a una rampa'); xlabel('tiempo'); grid; |
Respuesta impulso unitario de sistemas de primer orden.
Nuevamente, teniendo como punto de partida la ecuación (5),
$$\frac{Y(s)}{x(s)}=\frac{1}{Ts+1}$$
Tenemos que la transformada de Laplace del impulso unitario es igual a 1, vamos a someter a nuestro sistema a esta entrada, es decir:
$$y(s)=\frac{1}{Ts+1}\cdots\cdots(20)$$
Aplicando Laplace a (20), tenemos:
$$y(t)=\mathcal{L}^{-1}\left \{ \frac{1}{Ts+1} \right \}\cdots\cdots(21)$$
Para resolver (21) es necesario normalizar la ecuación, por lo que dividimos todo el lado derecho entre $T$, obteniendo:
$$\frac{\frac{1}{T}}{\frac{Ts}{T}+\frac{1}{T}}=\frac{\frac{1}{T}}{s+\frac{1}{T}}\cdots\cdots(22)$$
Sustituyendo (22) en (21), tenemos:
$$y(t)=\frac{1}{T}\mathcal{L}^{-1}\left \{ \frac{1}{s+\frac{1}{T}} \right \}\cdots\cdots(23)$$
Aplicando $\mathcal{L}^{-1}$ a (23):
$$y(t)=\frac{1}{T}e^{\frac{-t}{T}}\cdots\cdots(24)$$
La ecuación (24) es la representación general del sistema de primer orden en respuesta a una entrada impulso unitario.
El comportamiento de un impulso unitario dentro del sistema, puede verse en la figura 4, donde se ve que la ecuación (24) define el tiempo de regreso al estado inicial.
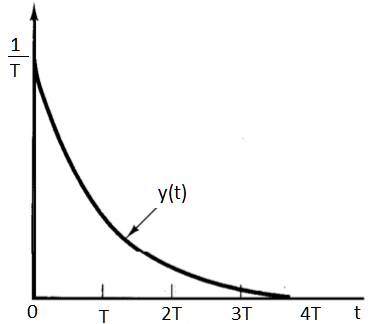
Fig. 4.- Curva de respuesta de un sistema de primer orden a una entrada impulso.
Para graficar la salida de un sistema de primer orden cuando se ingresa un pulso unitario, se sigue el siguiente código de Matlab:
|
1 2 3 4 5 6 7 8 9 10 |
K=1; tau=1; num=K; den=[tau 1]; t=[0:0.1:10]; salida=impulse(num,den,t); plot(t,salida) title('Respuesta a un impulso'); xlabel('tiempo'); grid; |
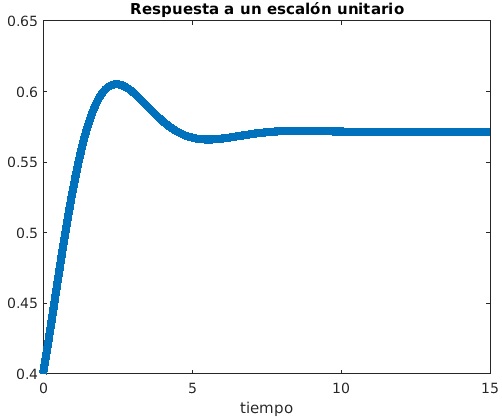
Para ingresar sistemas reales, basta con ingresar los coeficientes del denominador y del denominador de la función de transferencia, por ejemplo:
|
1 2 3 4 5 6 7 |
num=[2 3 4]; den=[5 6 7]; t=[0:0.1:15]; salida=step(num,den,t); plot(t,salida,"LineWidth",6); title('Respuesta a un escalón unitario'); xlabel('tiempo'); |
Este código da como resultado la figura 5.
Fig. 5.- Gráfica obtenida por medio de código de Matlab.