Sistema de segundo orden: Resorte, Masa, Amortiguador
De acuerdo a otra página de esta web, el lector debe de estar familiarizado con los sistemas de segundo orden.
Supongamos que tenemos el siguiente sistema de segundo orden:
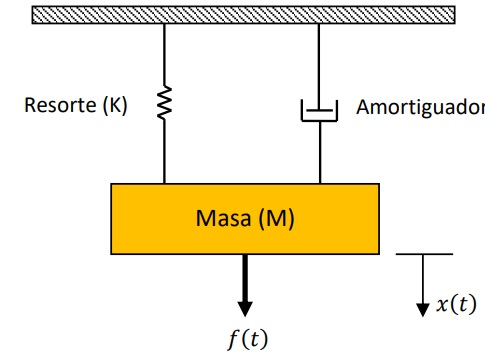
Fig. 1.- Sistema de segundo orden Resorte, Masa, Amortiguador.
Para modelar el sistema de la figura 1, es necesario auxiliarnos de la segunda Ley de Newton, que nos dice:
$$\sum Fuerzas=m*a$$
Considerando las funciones de velocidad y aceleración aplicadas en la masa, podemos expresar el comportamiento de la masa en el sistema en la forma:
$$
\begin{equation}
M\frac{d^{2}x(t)}{dt}=f(t)-D\frac{dx(t)}{dt}-Kx(t)
\end{equation}
$$
Ahora bien, si dividimos toda la ecuación entre M, tenemos
$$
\begin{equation}
\frac{d^{2}x(t)}{dt}=\frac{f(t)}{M}-\frac{D}{M}\frac{dx(t)}{dt}-\frac{K}{M}x(t)
\end{equation}
$$
Si aplicamos la transformada de Laplace, considerando condiciones iniciales iguales a cero (Formulario se puede ver aquí) a la ecuación (2), tenemos:
$$
\begin{equation}
S^{2}X(S)=-\frac{D}{M}SX(S)-\frac{K}{M}X(S)+\frac{F(S)}{M}
\end{equation}
$$
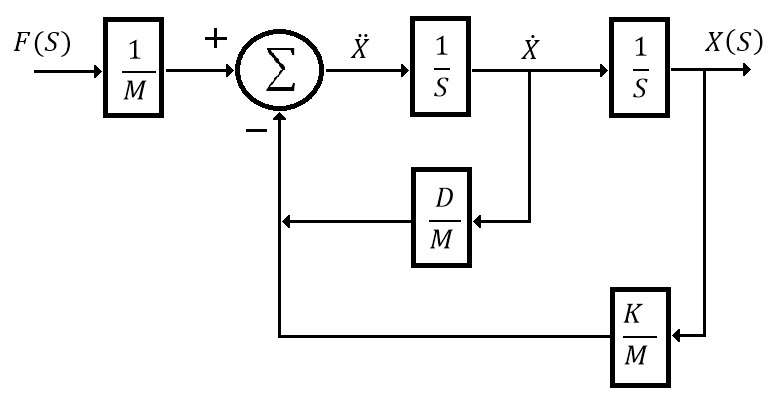
El sistema de la ecuación (3), puede ser representado por medio del siguiente esquema:
Fig.2.- Esquema representativo de un sistema de segundo orden, este responde a la ecuación (3).
Es posible ver en el diagrama de la figura 2 como después de la sumatoria se forma la ecuación (3), donde $\dot{x}$ y $\ddot{x}$ son la primera y segunda derivada de X, respectivamente.
De (3), colocamos todos los elementos que contengan X(S) de un solo lado de la igualdad
$$
\begin{equation}
\frac{F(S)}{M}=S^{2}X(S)+\frac{D}{M}SX(S)+\frac{K}{M}X(S)
\end{equation}
$$
Ahora bien, de (4) agrupamos y factorizamos X(S), tal que
$$
\begin{equation}
\frac{F(S)}{M}=\left [ S^{2}+\frac{D}{M}S+\frac{K}{M}\right ]X(S)
\end{equation}
$$
Obteniendo la función de transferencia, tenemos
$$
\begin{equation}
\frac{X(S)}{F(S)}= \frac{\frac{1}{M}}{S^{2}+\frac{D}{M}S+\frac{K}{M}}
\end{equation}
$$
Por la ecuación estándar de los sistemas de segundo orden, sabemos que el coeficiente en el numerador debe de ser igual al coeficiente independiente del denominador, por lo tanto multiplicamos el cociente del numerador de (6) por un uno algebraico, tal que:
$$\left ( \frac{K}{K}\right )\left ( \frac{1}{K}\right )\rightarrow\left ( \frac{1}{K}\right )\left ( \frac{K}{M}\right )$$
Obteniendo:
$$
\begin{equation}
\frac{X(S)}{F(S)}= \frac{\left (\frac{1}{K} \right )\left ( \frac{K}{M}\right )}{S^{2}+\frac{D}{M}S+\frac{K}{M}}=\left ( \frac{1}{K}\right )\left[\frac{\left ( \frac{K}{M}\right )}{S^{2}+\frac{D}{M}S+\frac{K}{M}}\right]
\end{equation}
$$
En la ecuación (7) se puede observar que los dos coeficientes previamente mencionados ya son iguales, y vemos en el denominador que ya tenemos un polinomio de segundo grado. Por lo tanto, la ecuación (7) la podemos pasar a la ecuación característica de un sistema de segundo orden, tal que:
$$\frac{X(S)}{F(S)}=k\frac{\omega_{n}^{2}}{S^{2}+2\zeta\omega_{n}S+\omega_{n}^{2}}$$
Donde:
$$\omega_{n}^{2}=\frac{K}{M}$$
$$2\zeta\omega_{n}=\frac{D}{M}$$
$$k=\frac{1}{K}$$
A partir de estos valores, se pueden calcular las características que definirán a cualquier sistema de segundo orden.
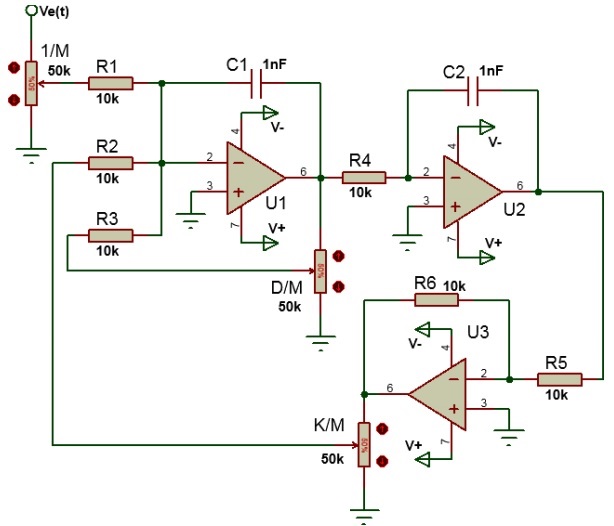
Es importante mencionar, que el sistema modelado puede ser representado de manera electrónica por medio del circuito que se muestra a continuación.
Fig. 3.- Representación electrónica del sistema de segundo orden mostrado en la figura 1.