Robótica móvil

Uno de los tipos particulares dentro del universo que engloba la robótica, es la robótica móvil. En esta sección se revisarán algunos de los aspectos base de los robots móviles

Para ingresar al tema, primero que nada se debe de repasar el concepto de vector y sus características.

Un vector es un conjunto ordenado de $n$ números reales. Se representa por una flecha o un punto en el espacio de dimensión $n$, y es bien conocido porque tiene magnitud, dirección y sentido.
Se define a un vector columna de [n $\times$ 1] como:

$$
V=\left[
\begin{array}{c}
v_{1} \\
\vdots \\
v_{n}%
\end{array}%
\right]
$$
y a un vector fila de [1 $\times$ n] como:
$$
V=\left[
\begin{array}{ccc}
v_{1} & \cdots & v_{n}%
\end{array}%
\right]
$$

En la figura 1, se puede ver la representación gráfica de un vector de dos dimensiones.

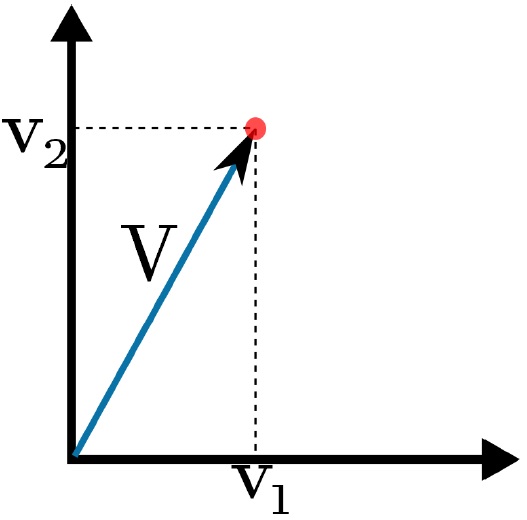Fig. 1.- Vector en un espacio 2D.

Operaciones con vectores:

Se pueden realizar diferentes operaciones aritméticas con los vectores, tales como:

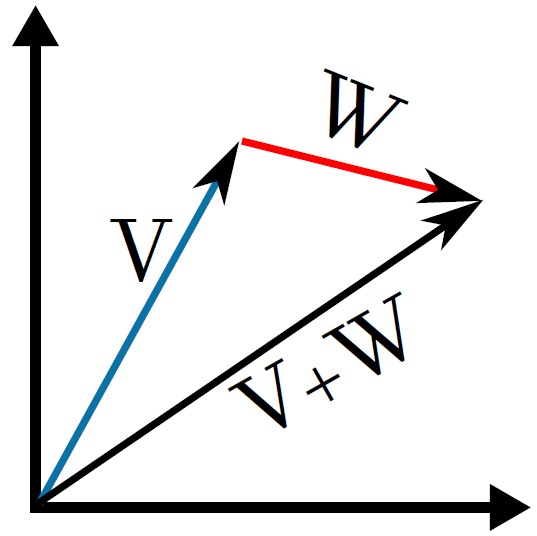
• Suma y Resta: Los vectores pueden ser sumados matemáticamente en la siguiente forma:

  $$
  \left[
  \begin{array}{c}
  v_{1} \\
  v_{2}%
  \end{array}%
  \right] \pm \left[
  \begin{array}{c}
  w_{1} \\
  w_{2}%
  \end{array}%
  \right] =\left[
  \begin{array}{c}
  w_{1} \\
  w_{2}%
  \end{array}%
  \right] \pm \left[
  \begin{array}{c}
  v_{1} \\
  v_{2}%
  \end{array}%
  \right] =\left[
  \begin{array}{c}
  v_{1}\pm w_{1} \\
  v_{2}\pm w_{2}%
  \end{array}%
  \right]
  $$
  lo que gráficamente se puede ver como la figura 2,

  Fig.2.- Suma de vectores.

• Multiplicación  de un vector por un escalar. Esta operación cambia la magnitud del vector, pero no su dirección, tal que:
  $$
  kV=k\left[
  \begin{array}{cc}
  v_{1} & v_{2}%
  \end{array}%
  \right] =\left[
  \begin{array}{cc}
  kv_{1} & kv_{2}%
  \end{array}%
  \right]
  $$
  donde $k$ es una constante, gráficamente se puede ver tal como la figura 3.

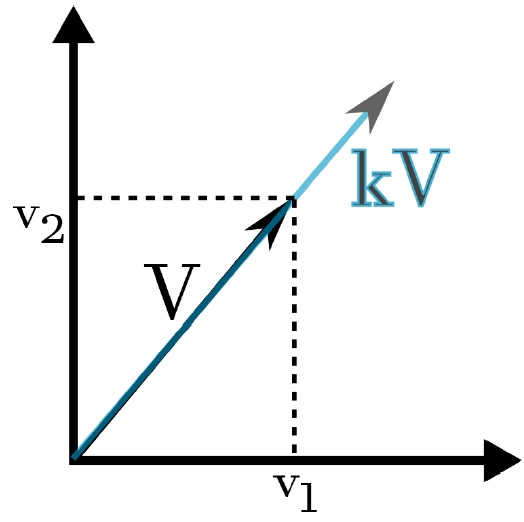Fig. 3.- Multiplicación de un vector por un valor escalar.

• Magnitud: esta operación sirve para obtener la longitud total del vector, tal que:
  $$
  \left\Vert V\right\Vert =\sqrt{v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}
  $$
• Normalización: sirve para obtener el vector unitario y sirve para conocer la dirección de un vector sin importar su longitud, en la forma:
  $$
  \hat{V}=\frac{V}{\left\Vert V\right\Vert }
  $$
• La magnitud y la normalización pueden observarse en la figura 4.

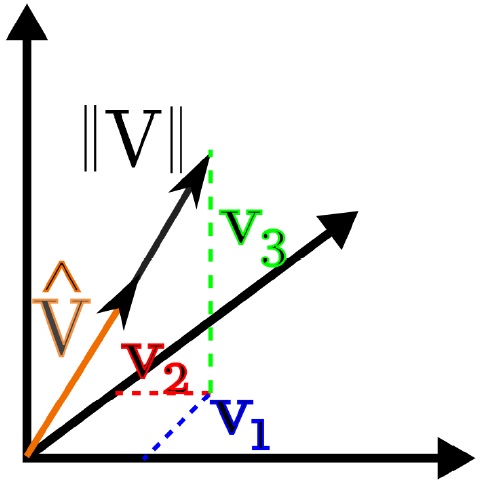Fig. 4.- Magnitud de un vector (negro), y normalización del mismo vector (naranja).

• Producto punto. Este producto de vectores es una proyección de un vector $V$ sobre el vector $W$, también puede servir para medir el ángulo entre estos vectores como se ve a continuación:
  $$
  V\cdot W=VW\cos \theta
  $$
  lo cual también puede ser visto de la forma,

$$\begin{eqnarray*}
V\cdot W&=&\left[
\begin{array}{ccc}
v_{1} & v_{2} & v_{3}%
\end{array}%
\right] \left[
\begin{array}{c}
w_{1} \\
w_{2} \\
w_{3}%
\end{array}%
\right] \\
&=&v_{1}w_{1}+v_{2}w_{2}+v_{3}w_{3}=\sum\limits_{i}v_{i}w_{i}
\end{eqnarray*}$$

además, si los vectores son ortogonales, tenemos que $V\cdot W=0$.

La representación gráfica del producto punto la podemos ver en la figura 5.

Fig.5.- Producto punto entre vectores.

• Producto cruz. Este producto de vectores da como resultado un vector perpendicular al plano de los vectores $V$ y $W$, donde la magnitud del vector resultante depende del área del paralelogramo formado por los vectores $V$ y $W$, como se ve a continuación.
  $$
  U=V\times W
  $$
  y
  $$
  \left\Vert V\times W\right\Vert =\left\Vert V\right\Vert \left\Vert
  W\right\Vert \sin \theta
  $$

La representación gráfica del producto cruz la podemos ver en la figura 6.

Fig.6.- Producto cruz entre vectores.

Matrices y sus operaciones

Otro concepto importante de recordar es el de la matriz, la importancia que estas juegan en la dinámica y cinemática de un robot es primordial para el diseño y comportamiento de cualquier elemento robótico.

Una matriz es un conjunto de números ordenados en filas y columnas. El tamaño de la matriz se denota siempre como filas $\times$ columnas, como se muestra a continuación:

$$
A_{nm}=
\left[
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1m} \\
a_{21} & a_{22} & \cdots & a_{2m} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nm}%
\end{array}%
\right] ~\ \ \ \ \ \ \ A:n(filas) \times m(columnas)
$$
Las matrices siguen las mismas operaciones definidas anteriormente en los vecores, solo se debe recordar que en la suma la conmutatividad y la asociatividad se cumplen, mientras que la multiplicación en las matrices no es conmutativa. Podemos obtener diferentes propiedades de estas tales como:

• Traspuesta. En esta operación se invierten las filas por las columnas en una matriz. Sea una matriz $A$ de $n \times m$,
  $$
  A=\left[
  \begin{array}{cccc}
  a_{11} & a_{12} & \cdots & a_{1m} \\
  a_{21} & a_{22} & \cdots & a_{2m} \\
  \vdots & \vdots & \ddots & \vdots \\
  a_{n1} & a_{n2} & \cdots & a_{nm}%
  \end{array}%
  \right] ~\ \ \ \
  $$

la matriz traspuesta es denotada por $A^{T}$, y se muestra a continuación:

$$A^{T}=\left[
\begin{array}{cccc}
a_{11} & a_{21} & \vdots & a_{n1} \\
a_{12} & a_{22} & \vdots & a_{n2} \\
\cdots & \cdots & \ddots & \cdots \\
a_{1m} & a_{2m} & \vdots & a_{nm}
\end{array}
\ \right] $$
note como en la transpuesta de $A$ las filas ahora son columnas y viceversa.

Ya habiendo recordado los vectores y las matrices, podemos definir algunas características y acciones que se pueden realizar con los robots móviles, por ejemplo:

Cuerpo Rígido: Es un sistema que es capaz solo de desplazamientos.

Desplazamiento: Es un cambio en la configuración del sistema que preserva de igual forma la distancia y la orientación del sistema.

Rotación: Es un movimiento en sentido antihorario de un cuerpo rígido con respecto a un punto fijo. A continuación se muestran las matrices de rotación con respecto a los ejes $x$, $y$, $z$.
$$
R_{x}(\theta )=\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta
\end{array}%
\right]
$$
$$
R_{y}(\theta )=\left[
\begin{array}{ccc}
\cos \theta & 0 & -\sin \theta \\
0 & 1 & \\
\sin \theta & 0 & \cos \theta
\end{array}%
\right]
$$

$$
R_{z}(\theta )=\left[
\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1%
\end{array}%
\right]
$$

En la figura 7 se puede observar la rotación de un cuerpo rígido con respecto a un punto.

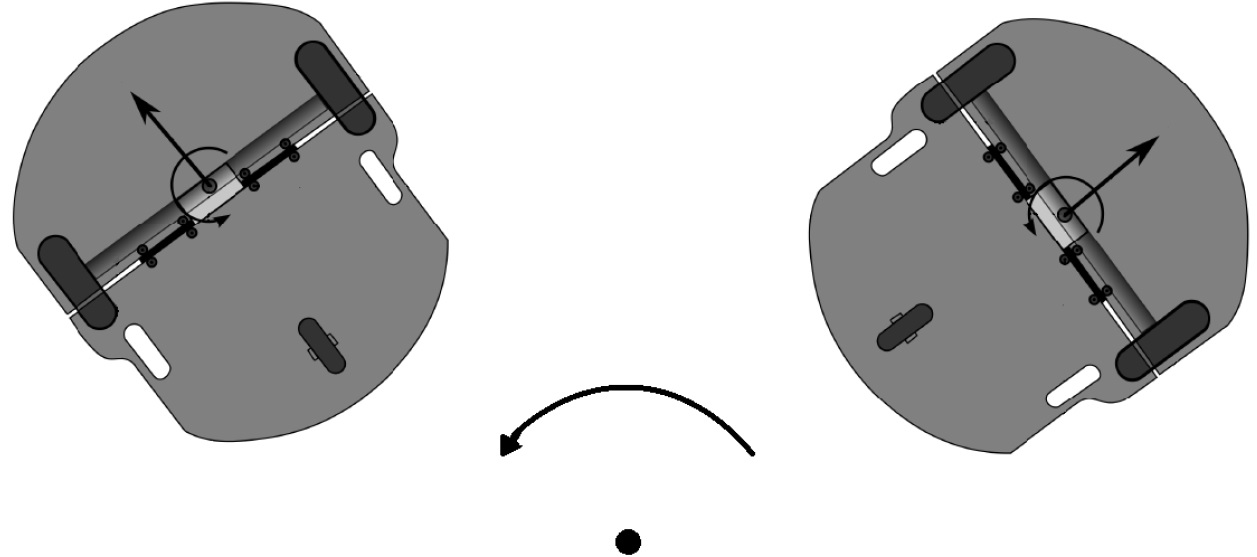Fig. 7.- Rotación de un cuerpo rígido, robot móvil, con respecto al punto que se ve en la parte inferior de la figura.

Traslación: Es un desplazamiento de todos los puntos moviéndose distancias iguales en líneas paralelas, tal que:

$$
p=\left[
\begin{array}{c}
t \\
1%
\end{array}%
\right]
$$
donde,
$$
t=\left[
\begin{array}{c}
x \\
y \\
z \\
\end{array}%
\right]
$$

En la figura 8, se puede apreciar la traslación de un cuerpo rígido.

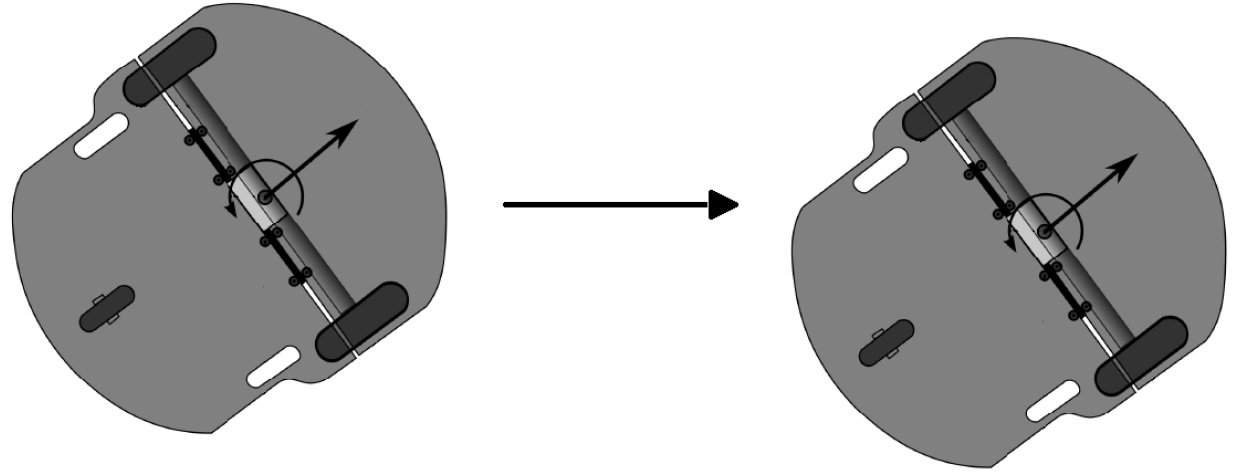Fig. 8.-  Traslación de un cuerpo rígido, robot móvil.

• Al juntar la matriz de rotación y el vector traslación se obtiene:
  $$
  A=\left[
  \begin{array}{cc}
  R & t \\
  0 & 1%
  \end{array}%
  \right]
  $$Espacio de configuración (C-Space). El espacio de configuración es el ambiente donde se mueven los robots móviles, se caracteriza por los grados de libertad que cada ambiente pueda otorgar a los robots y la configuración que tenga cada ambiente, sirve para la localización de la posición y orientación de los robots. Algunos ejemplos son:
• Tren, 1-D C-space. $x$
• Automóvil, 2-D C-space. $x,y,\theta$
• Aeronave, 3-D C-space. $x,y,z,\phi,\theta,\psi$

Grados de libertad: Número de variables independientes necesarias para especificar la posición y orientación. Algunos ejemplos pueden verse en la tabla 1.

Tabla 1.-Ejemplos de grados de libertad según el sistema.

Cinemática: Del griego: $\kappa \iota \upsilon \eta \mu \alpha $ kín$\bar{e}$ma, significa movimiento. Rama de la física que estudia el movimiento prescindiendo de las fuerzas que lo producen.

Esto concierne tanto a la cinemática directa como a la inversa de los robots móviles. Para poder conocer correctamente la posición y orientación de los robots móviles es necesario ocupar diversos sensores, ya que si solo se ocupan los encoders para conocer la posición y trayectoria que ha seguido el robot móvil, será difícil medir correctamente esto ya que se van acumulando los errores en la estimación de la posición.

Cinemática directa.

•  Transformación del movimiento de los actuadores (motores, llantas), es decir velocidad lineal y angular, a posiciones físicas en el espacio.
•  Asumiendo que se conoce la posición inicial y la función de control es posible encontrar la posición final del robot.

Cinemática inversa.

• Transforma las posiciones del robot a velocidades lineal y angular.
• Se requiere para el control del movimiento.
• Asumiendo que se conoce la posición inicial y final del robot, es posible encontrar una función de control que lleve al robot de la posición inicial a la final.

Robótica Móvil

Esta rama de la robótica estudia el la alteración espacial de los robots móviles desde la perspectiva de su cinemática, para poder realizar un control de la trayectoria que sigan y el trabajo a realizar.

Cinemática directa e inversa de un robot móvil.

Considere que $q_{1},q_{2},…,q_{n}$ son las coordenadas generalizadas del espacio de los actuadores y que $x_{1},x_{2},…,x_{n}$ son las del espacio de trabajo, tenemos que
$$
q=
\begin{bmatrix}
q_{1}\\
q_{2}\\
\vdots\\
q_{n}
\end{bmatrix}, \ \ \ \ \
p=
\begin{bmatrix}
x_{1}\\
x_{2}\\
\vdots\\
x_{n}
\end{bmatrix}
$$
el problema de determinar $p$ (posición) a partir de conocer $q$ (velocidades) se conoce como problema de cinemática directa, mientras que encontrar $q$ a partir de $p$ se conoce como cinemática inversa.

La cinemática directa es definida como:

$$
p=f(q), \ \ \ \ \ \
f(q)=
\begin{bmatrix}
f_{1}(q) \\
f_{2}(q) \\
\vdots \\
f_{m}(q)
\end{bmatrix}
$$

Mientras que la cinemática inversa esta definida en la siguiente forma:

$$
q=f^{-1}(p)
$$

Parar lograr esto es necesario conocer la relación diferencial que hay entre $q$ y $p$, a esto se le llama la cinemática diferencial directa, definida por:

$$
dp=Jdq
$$

donde,

\begin{eqnarray}
dq&=&
\begin{bmatrix}
dq_{1} \\
\vdots \\
dq_{n}
\end{bmatrix},
\label{eqdpdq1} \\
dp&=&
\begin{bmatrix}
dx_{1} \\
\vdots \\
dx_{m}
\end{bmatrix}
\label{eqdpdq2}
\end{eqnarray}

y la matriz $J$ de $m \times n$,
\[
J=\begin{bmatrix}
\frac{\partial x_{1}}{\partial q_{1}} & \frac{\partial x_{1}}{\partial q_{2}} & \cdots & \frac{\partial x_{1}}{\partial q_{n}} \\
\vdots & \vdots & \vdots & \vdots \\
\frac{\partial x_{1}}{\partial q_{1}} & \frac{\partial x_{1}}{\partial q_{2}} & \cdots & \frac{\partial x_{1}}{\partial q_{n}}
\end{bmatrix}=\left[J_{ij}\right]
\]
es conocida como la matriz Jacobiana del robot móvil. Representa la relación entre los movimientos de los actuadores con el movimiento del robot en el espacio.

Si dividimos (eqdpdq1) y (eqdpdq2) con respecto a $dt$ entonces se obtiene formalmente,
\[
\frac{dp}{dt}=J\frac{dq}{dt}
\]
es decir,
\[
\dot{p}=J\dot{q}
\]

Si se asume que $m=n$, es decir, que la matriz $J$ sea cuadrada y existe la inversa de esta matriz, entonces,

• \[
  \dot{q}=J^{-1}\dot{p}
  \]Si $m\neq n$, es decir, que la matriz $J$ no es cuadrada, se está en el caso de que la posición del robot está sobre caracterizada y alguna de las coordenadas utilizadas pueden soslayar, o estamos en el caso que con una misma coordenada puede obtenerse diversas posiciones en el espacio, debido a que está sub caracterizada la posición, tal que:
•  $m>n \ \ \ \rightarrow \ \ \ \dot{q}$ está sobre especificado y se utiliza la inversa generalizada.
• $m<n \ \ \ \rightarrow \ \ \ \dot{q}$ está sub especificada. Diferentes $\dot{q}$ dan la misma $\dot{p}$

Para poder definir claramente la posición en el espacio del robot, se deben utilizar marcos de referencia, para esto se debe notar lo siguiente,

• Se usa la convención de la mano derecha.
• Marco inercial.

$\rightarrow$ Fijo, usualmente es la tierra.

• Marco Cuerpo.

$\rightarrow$ Fijo al vehículo. Centro de gravedad, masa o rotación.

• Marco sensor.

$\rightarrow$ Fijo en el sensor, convenientemente puesto para obtener las mediciones.

• Los diferentes marcos de referencia se pueden apreciar en la figura 9.

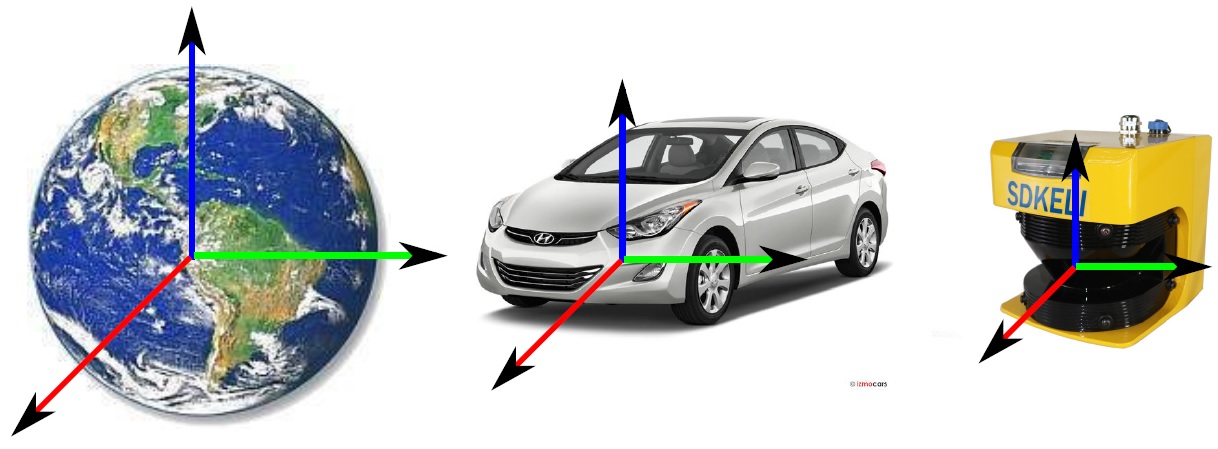Fig. 9.- Distintos marcos de referencia.

Esto es útil para realizar las transformaciones necesarias de la posición de los sensores, actuadores, cuerpos rígidos con respecto al punto de control designado en el robot móvil, ta como se puede ver en la figura 10.

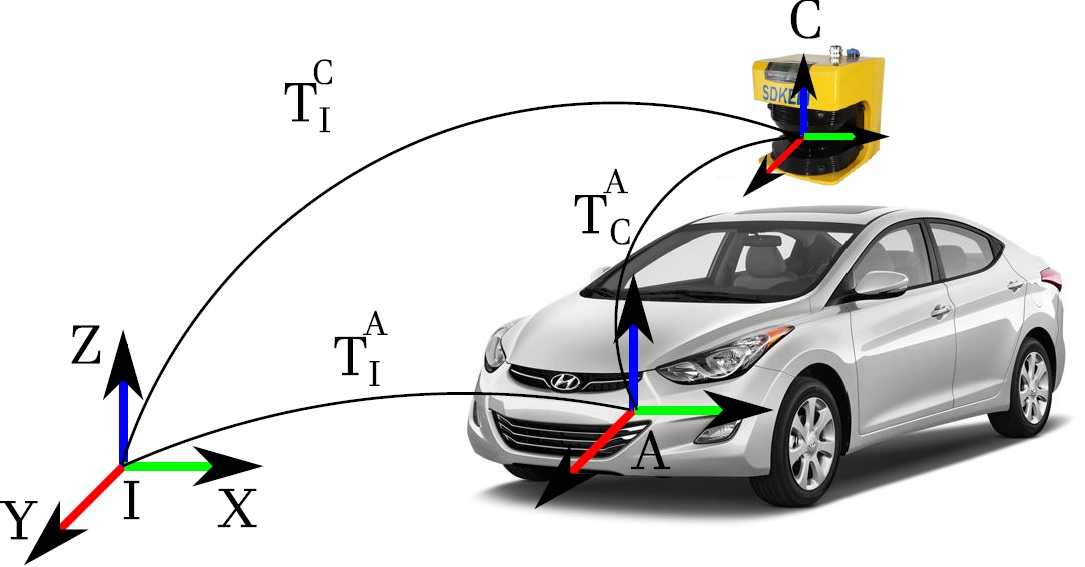Fig. 10.- Relación entre los distintos marcos de referencia.

Modelos matemáticos.

Se modela matemáticamente el comportamiento cinemático de un robot móvil, para esto, imagine una moneda que rueda sobre el plano, como se muestra en la figura 11.

Fig. 11.-Movimiento de una moneda en el plano.

En la figura 11 se puede observar dicha moneda, suponga además que la moneda no se derrapa, ni se desliza hacia los lados, tampoco se tambalea y por lo tanto siempre se desplaza de manera vertical sobre el plano. La moneda tiene un radio $r$ y su movimiento angular está dado por $\theta$, mientras que la orientación que tiene en el plano $X-Y$ es dada por $\phi$, y su posición está dada por las coordenadas $(x,y)$.

A partir de la Figura 11, se obtienen los parámetros que sirven para conocer el movimiento de la moneda, estos parámetros son, su posición en el plano dada por las coordenads $(x,y)$, su orientación $\phi$ y su ángulo $\theta$, es decir,
$$
q=(x,y,\theta,\phi)
$$
La velocidad con la que se mueve cada uno de estos parámetros, se puede obtener al analizar la Figura 11, y se obtiene la siguiente relación,
$$
\dot{q}=\begin{bmatrix}
\dot{x}\\
\dot{y} \\
\dot{\phi} \\
\dot{\theta}
\end{bmatrix}=\begin{bmatrix}
r\cos\phi & 0 \\
r\sin\phi & 0 \\
1 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
u_{1} \\
u_{2}
\end{bmatrix}
$$

Esto es en el caso de una moneda o una llanta. Si ahora el mismo movimiento lo analizamos a partir de un cuerpo rígido como un robot móvil, se puede obtener el modelo cinemático del mismo, tal como se muestra en la figura 12.

Fig. 12.- Robot móvil en el plano $X-Y$

En la figura 13 se presenta la posición de un robot móvil en un plano $X-Y$, donde el radio de las llantas está representado por $r$, la distancia del punto medio del eje de las llantas a cualquiera de ellas está dada por $d$, la orientación del vehículo con respecto al eje $X$ está dada por $\theta$, la posición por $x,y$ y las velocidades lineal y angular están dadas por $V$ y $W$ respectivamente.

A partir de la figura 13 y siguiendo los hecho con la figura 11 se puede obtener la velocidad en cada uno de los parámetros del robot,
\begin{eqnarray}
\dot{q}=\begin{bmatrix}
\dot{x}\\
\dot{y} \\
\dot{\theta} \\
\dot{\phi_{L}} \\
\dot{\phi_{R}}
\end{bmatrix}=\begin{bmatrix}
\frac{r}{2}\cos\phi &\frac{r}{2}\cos\phi \\
\frac{r}{2}\sin\phi & \frac{r}{2}\sin\phi \\
-\frac{r}{2d} & \frac{r}{2d} \\
1 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
u_{L} \\
u_{R}
\end{bmatrix}
\label{mod1}
\end{eqnarray}

Note que ahora $\theta$ es la orientación que tenga el robot móvil con respecto al eje $X$, $\phi_{L}$ y $\phi_{R}$ es el ángulo de las llantas, además $u_{L}$ y $u_{R}$ son las velocidades angulares de las llantas izquierda y derecha respectivamente.

De la ecuación (mod1) es posible notar que la relación entre la velocidad angular de las llantas y la velocidad lineal y angular que tenga el vehículo es:

\begin{eqnarray}
v&=&\frac{r}{2}(u_{R}+u_{L})
\label{veltras}\\
w&=&\frac{r}{d}(u_{R}-u_{L})
\label{veltras1}
\end{eqnarray}

Con las ecuaciones veltras y veltras1 es posible reducir la ecuación mod1, de la siguiente forma,

\begin{eqnarray}
\dot{q}=\begin{bmatrix}
\dot{x}\\
\dot{y} \\
\dot{\theta}
\end{bmatrix}=\begin{bmatrix}
\cos\theta &0 \\
\sin\theta & 0\\
0 & 1
\end{bmatrix}\begin{bmatrix}
v \\
w
\end{bmatrix}
\label{modf}
\end{eqnarray}

La ecuación (modf) se conoce como el modelo cinemático de un robot móvil tipo diferencial. Es decir que cada una de sus ruedas tiene movimiento independiente, al tener un movimiento igual ambas ruedas, el robot avanza en línea recta, si una de las dos ruedas tienen velocidades diferentes, entonces el robot se mueve realizando una curva como trayectoria.

Por otra parte, se debe recordar que un robot diferencial al igual que un robot tipo automóvil, tienen ciertas restricciones en su movimiento, la principal de ellas es que no pueden desplazarse de manera lateral, siempre deben avanzar o retroceder y girar para alcanzar ciertos puntos, pero no pueden deslizarse hacia los lados. A esta restricción se le conoce como restricción no holónoma y matemáticamente se representa de la forma,

\begin{equation}
\dot{y}\cos\theta-\dot{x}\sin\theta=0
\end{equation}

Esto se debe a los componentes de velocidad de los vehículos, recordando la velocidad que tiene el vehículo en la coordenada $x$ e $y$,

$$\dot{x}=v\cos\theta$$
$$\dot{y}=v\sin\theta$$

Se puede notar que la velocidad de una coordenada va ligada a la de la otra coordenada, y esto restringe el cambio de velocidad independiente de las coordenadas.

Donde además se puede notar que la velocidad que sigue un vehículo siempre es tangente al trayecto que realiza, tal que:

$$\frac{dy}{dx}=\tan \theta= \frac{\sin \theta}{\cos \theta}
$$

De manera gráfica esto está representado por la figura 13.

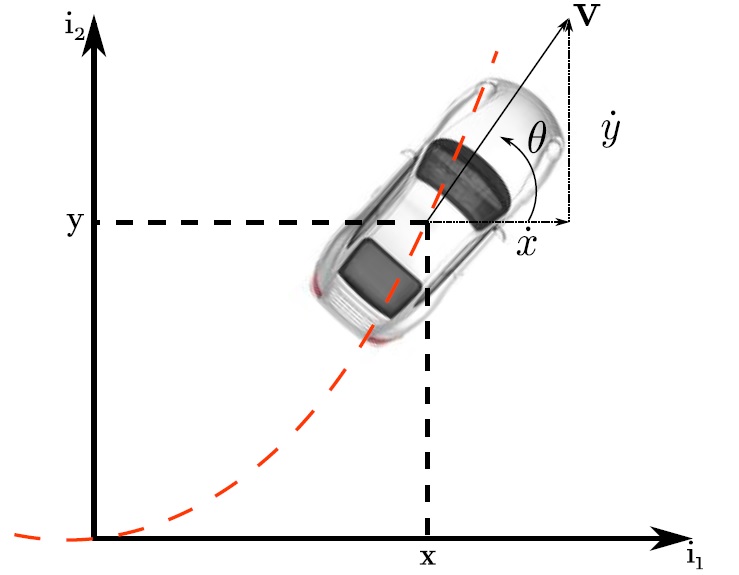Fig. 13.- Relación de la velocidad y trayectoria de un vehículo.

Mientras que en un robot diferencial, los movimientos hacia un lado u otro se hacen con una diferencia entre la velocidad de las ruedas, en el robot tipo automóvil, el movimiento se realiza al mover el eje de las llantas delanteras o traseras, esto se puede notar mejor en la figura 14,

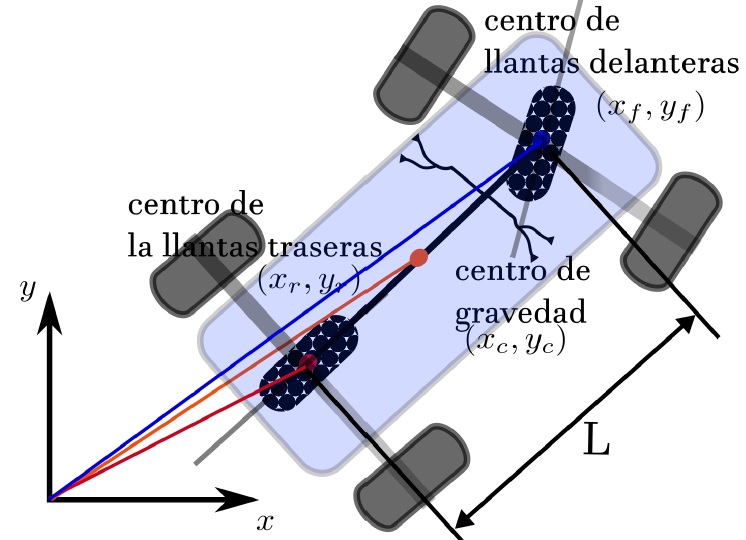Fig. 14.- Relación de las llantas delanteras, traseras y el centro de gravedad de un vehículo.

Donde es posible analizar que el comportamiento que tiene un vehículo es similar al movimiento que tendría una bicicleta, lo cual facilita el análisis para la obtención de su modelo cinemático.

Conforme se mueva el volante o el manubrio se realiza un giro , pero este giro no puede ser completo, hay un límite, este límite dependerá de el centro de rotación instantáneo que se genere, tal cómo se ve en la figura 15,

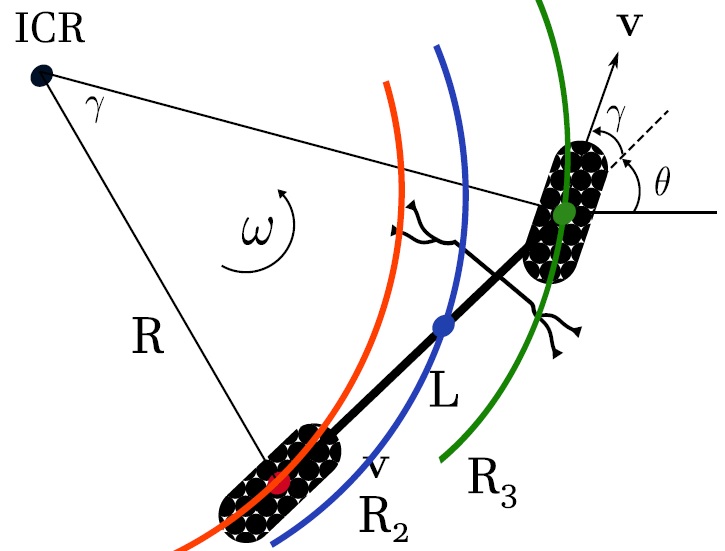Fig. 15.- Trayectoria seguida por cada punto de la bici, (eje delantero, trasero y gravedad) y centro de rotación instantáneo.

En la Figura 15 se observan las trayectorias seguidas por las llantas delanteras y traseras y además la trayectoria que sigue el centro de gravedad de la bici, dependiendo que tanto se mueva el manubrio, y si se extiende una línea colineal al eje de cada llanta, estas líneas tendrán una intersección en un punto llamado centro de rotación instantáneo (ICR, por sus siglas en inglés), el cual dependerá de la velocidad angular que tenga en ese momento el vehículo:

$$\dot{\theta}=\omega=\frac{v}{R}$$

Si se analiza la figura 15 utilizando triángulos semejantes, se nota que:

$$\tan \gamma=\frac{L}{R}$$

por lo tanto la ecuación de la velocidad de rotación que el vehículo lleva, está dada por:

$$\dot{\theta}=\omega=\frac{v}{R}=\frac{v \tan \gamma}{L}$$

Con esto es claro que habrá ciertos lugares a los que no puede llegar el vehículo si solo mueve el volante hacia una dirección y sin hacer maniobras, a esta área se le conoce como inaccesible para el robot y dependerá de las características del mismo, es to se puede observar en la figura 16.

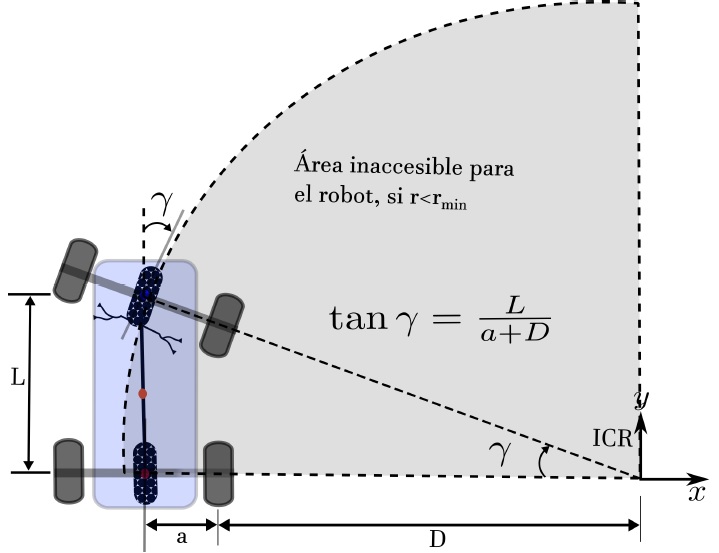Fig. 16.- Área inaccesible para un vehículo, dependiendo de sus características físicas.

El área inaccesible para el robot depende de la distancia $L$ que hay entre el eje delantero y el trasero, la distancia $a$ que hay entre el centro del eje trasero a cualquiera de sus llantas traseras y la distancia $D$ desde el punto de intersección ICR y la llanta trasera más cercana a ese punto, esto queda más claro al ver la figura 16.

Con estos análisis es posible obtener el modelo cinemático de un robot tipo  triciclo o de un vehículo común. El modelo cinemático esta dado por,

\begin{align*}
\dot{x} & = v \cos(\theta) \\
\dot{y} & = v \sin(\theta) \\
\dot{\theta} & = \frac{v}{L} \tan(\gamma)
\end{align*}