Reogramas
im Imagen recuperada de https://pixabay.com/es/illustrations/marca-marcador-mano-escribir-1577991/
Imagen recuperada de https://pixabay.com/es/illustrations/marca-marcador-mano-escribir-1577991/
Los reogramas pueden verse como una forma simplificada de un diagrama de bloques, en este caso, en lugar de ir desarrollando cada una de las interacciones de los bloques e ir generando un nuevo diagrama más simple que el anterior hasta llegar a la función de transferencia total (FT), en el reograma se utiliza una fórmula para llegar a dicha FT de forma más rápida. La fórmula utilizada es la fórmula de Mason, que nos dice que
$$FT=\frac{F(s)}{F(i)}=\frac{\sum_{k=1}^{N} P_k \Delta_k}{\Delta}$$
Dónde:
$$\Delta=1-\sum L_{a}+\sum L_{a}L_{b}-\sum L_{a}L_{b}L_{c}+\cdots +(-1)^{m}\sum\cdots +\cdots$$
$\sum L_a$ = Ganancia de lazo simple (sumatoria de todos los lazos del reograma).
$\sum L_{a}L_{b}$ = Ganancia de lazo doble (sumatoria de todos los producto de pares de lazos que no se tocan).
$\sum L_{a}L_{b}L_{c}$ = Ganancia de lazo triple (sumatoria de todos los producto de tercias de lazos que no se tocan).
$P_k$ = El $k$-esimo camino directo del reograma.
$\Delta_{k}$ = $\Delta$ evaluado considerando solo los lazos que no tocan el $k$-esimo camino directo del reograma.
$N$ = Número de caminos directos del reograma.
Para poder aplicar esta fórmula, es necesario identificar ciertos comportamientos dentro del diagrama de flujo de señales, primero que nada, es necesario identificar los caminos directos; Un camino directo es aquel que permite el paso sin interrupciones desde el punto de inicio hasta el punto final del reograma, este camino se define en función de las flechas de dirección de cada una de las ramificaciones existentes entre los nodos. Una vez encontrados los caminos directos, es necesario identificar los lazos; Un lazo es aquel que parte de un nodo $A$ y llega al mismo nodo $A$ de una forma natural y directa, es decir, las flechas de flujo te llevarán al nodo mencionado, sin interrupciones o repeticiones en algún punto.
Los elementos que componen un reograma, se muestra en la figura 1.
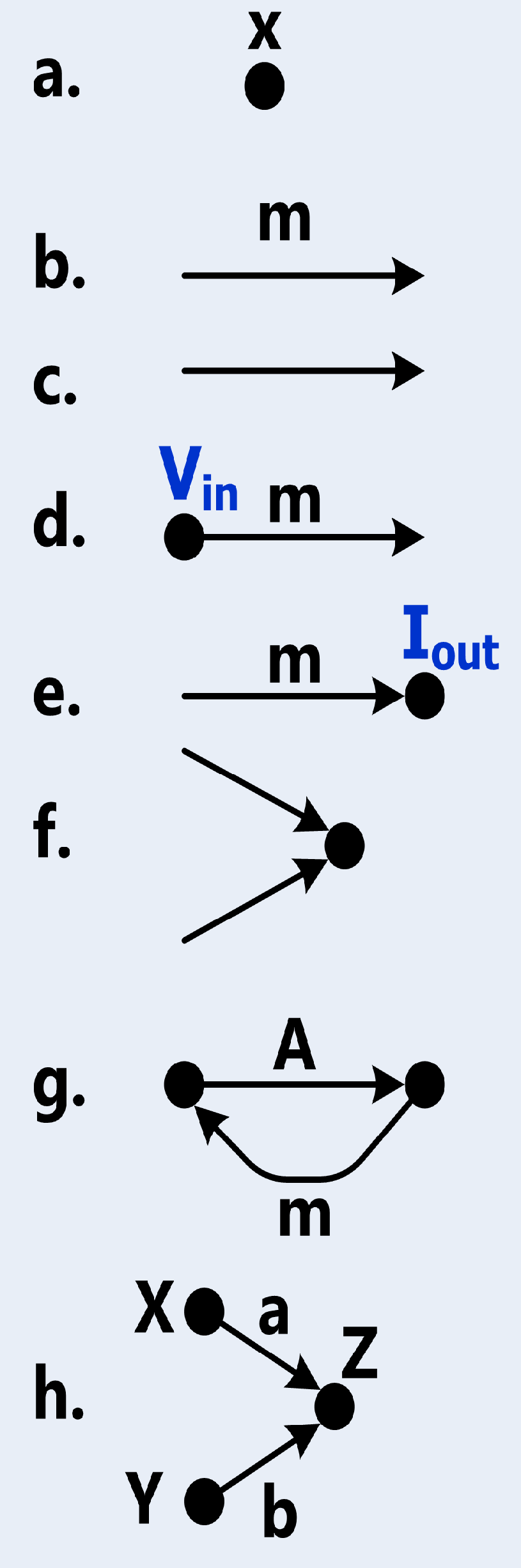
Fig. 1.- Elementos que componen una representación de diagramas de flujo de señal. a) Identificado como un nodo, b) Una ramificación con una ganancia $m$, c) Una ramificación con una ganancia igual a 1, d) Ramificación con la multiplicación $V_{in}\cdot m$, e) Nodo con una salida explicita, f) Un elemento de suma, g) Representación de un lazo simple, h) Representa la suma $Z=aX+bY$. Imagen obtenida de https://commons.wikimedia.org/wiki/File:Elements_of_a_signal_flow_graph.png
Para mostrar el comportamiento análogo entre los diagramas de bloques y los diagramas de flujo de señal, se utilizará la figura 2, en la cual se muestra una representación en bloques y una en flujo.
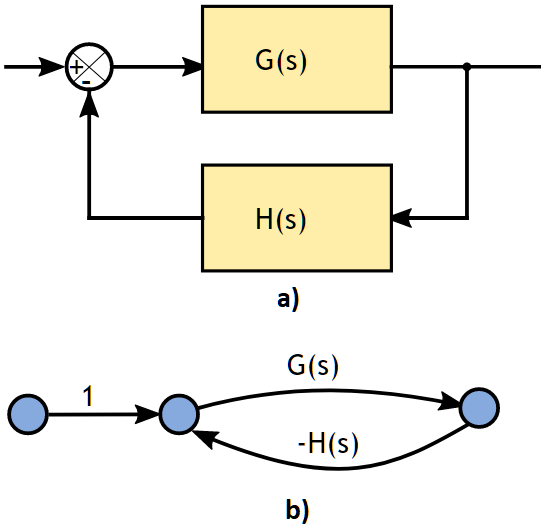
Fig. 2.- Comportamiento análogo entre a) un diagrama de bloques y b) un diagrama de flujo de señal.
En el caso de a) de la figura 2, sabemos que esta representación de retroalimentación puede ser resuelta por medio de la fórmula 13, del conjunto de reglas que se puede ver aquí, dando como resultado:
$$FT=\frac{G(S)}{1+G(S)H(S)}$$
Ahora bien, si utilizamos la regla de Mason para definir la función de transferencia del flujograma de la figura 2 b), vemos que primero hay que obtener los caminos directos y los lazos, en este caso el único camino directo está definido por $P_{1}=1\cdot G(S)$, y el diagrama solo cuenta con un lazo, definido por $L_{1}=–H(S)G(S) $, a partir de aquí, se puede calcular $\Delta_1$ correspondiente al camino directo $P_1$, tal que $\Delta_{1}=1-\sum L_{a}=1$, ya que $L_a$ corresponde a todos los lazos que no tocan al camino $P_1$, sin embargo, en este caso no existe lazo que cumpla con tal condición. Aplicando la regla de Mason al diagrama de la figura 2, tenemos:
$$FT=\frac{F(s)}{F(i)}=\frac{\sum_{k=1}^{N} P_k \Delta_k}{\Delta}= \frac{G(S)}{1-(-H(S)G(S))}= \frac{G(S)}{1+H(S)G(S)}$$
Es posible observar que la FT resultante tanto del diagrama de bloques como del flujograma es el mismo.
Para hacer más visible el uso de la fórmula de Mason, se resolverá el diagrama de la figura 3.
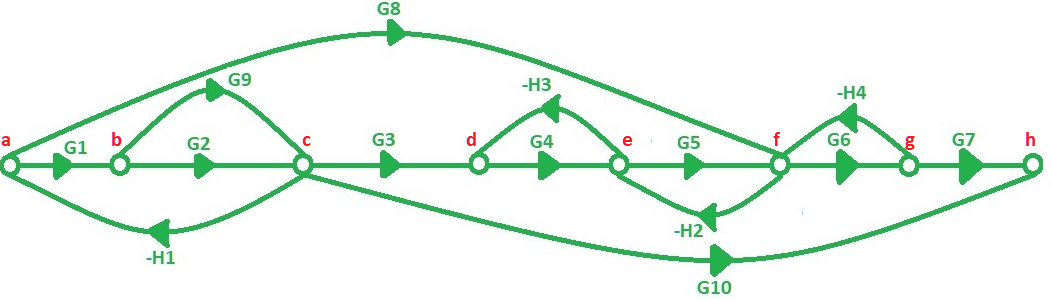
Fig. 3.- Reograma a resolver.
Para el diagrama de la figura 3, primero que nada, es necesario visualizar y definir los caminos directos que existen entre el nodo $a$ y el nodo $h$, inicio y término del diagrama, respectivamente.
En la figura 4 se pueden ver los 4 caminos directos que se pueden encontrar.
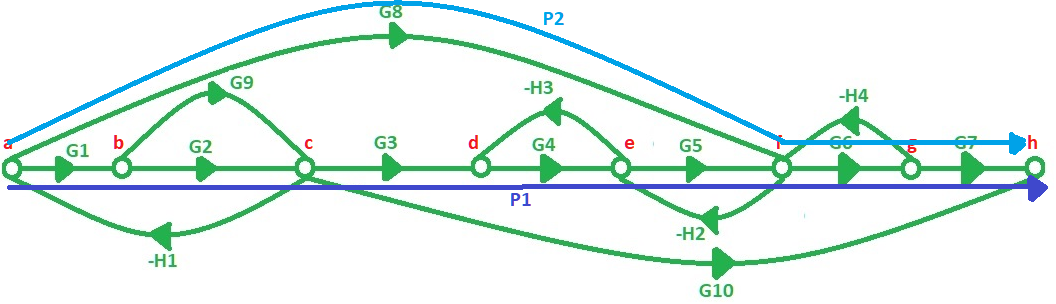
a)
b)
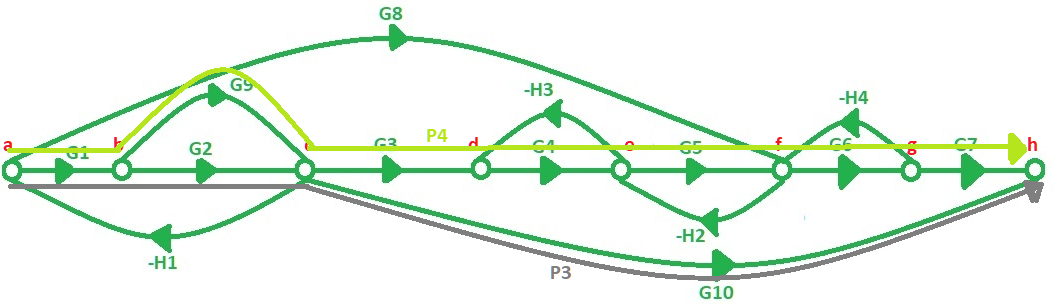
Fig. 4.- Visualización de los caminos directos que tiene el diagrama de flujo de señal. a) Muestra os caminos $P_1$ y $P_2$, b) Muestra los caminos $P_3$ y $P_4$.
Los caminos directos de la figura 4, se denominan como:
$$P_{1}=G_{1}G_{2}G_{3}G_{4}G_{5}G_{6}G_{7}$$
$$ P_{2}=G_{8}G_{6}G_{7}$$
$$P_{3}=G_{1}G_{2}G_{10}$$
$$P_{4}=G_{1}G_{9}G_{3}G_{4}G_{5}G_{6}G_{7}$$
Ahora, es necesario encontrar los lazos dentro del diagrama, los que se pueden observar en la figura 5.
a)
 b)
b)
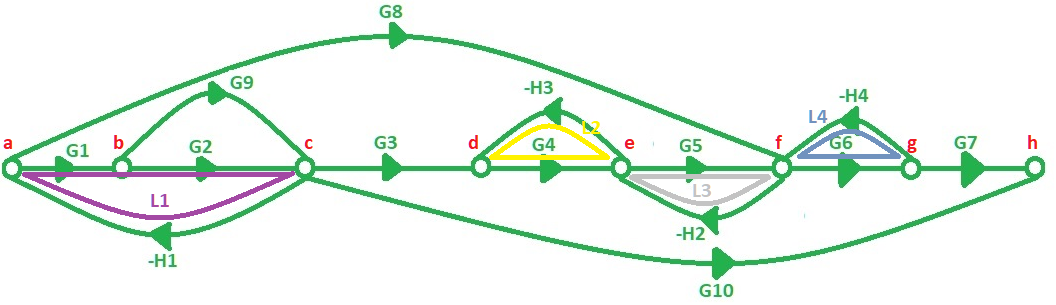
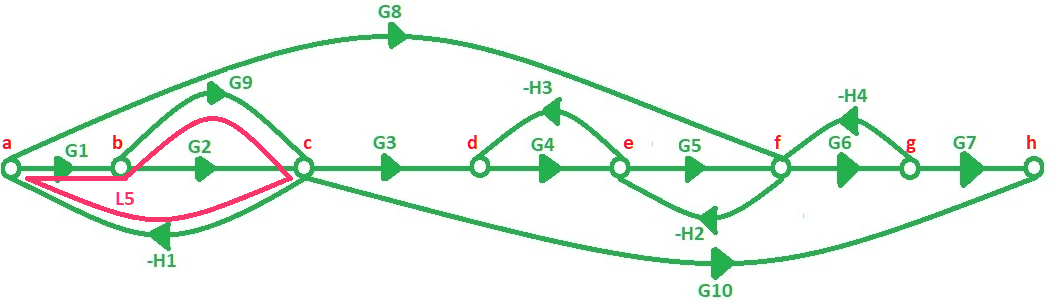
Fig. 5.- Lazos del diagrama de flujo de señales. a) Muestra los lazos 1 al 4, b) Muestra el lazo 5, que está un poco más “escondido” que los demás.
De acuerdo a los lazos identificados en la figura 5, los podemos definir como:
$$L_{1}=-H_{1}G_{1}G_{2}$$
$$L_{2}=-H_{3}G_{4}$$
$$L_{3}=-H_{2}G_{5}$$
$$L_{4}=-H_{4}G_{6}$$
$$L_{5}=-H_{1}G_{1}G_{9}$$
De este conjunto de lazos, podemos identificar pares de ellos que no se tocan entre si (en ningún punto ni nodo), tal que:
$$L_{1}L_{2}$$
$$L_{1}L_{3}$$
$$L_{1}L_{4}$$
$$L_{2}L_{4}$$
$$L_{5}L_{2}$$
$$L_{5}L_{3}$$
$$L_{5}L_{4}$$
En la misma manera, podemos identificar tercias de ellos que no se tocan entre si (en ningún punto ni nodo), tal que:
$$L_{1}L_{2}L_{4}$$
$$L_{5}L_{2}L_{4}$$
Este proceso lo seguiríamos realizando si el reograma tuviera los suficientes lazos para seguir armando conjuntos de 4 lazos que no se tocan, 5 lazos, etc.
Una vez que hemos determinado todos sus componentes, podemos calcular los valores de $\Delta_k$, recordando que se calcula un valor de delta para cada uno de los caminos directos, por lo que tenemos 4 deltas.
$$\Delta_{1}=1$$
Este valor de uno es debido a que $P_1$ toca a todos los lazos, por lo tanto no se le agrega ninguno de ellos a la expresión.
$$\Delta_{2}=1-L_{2}$$
Este resultado se da debido a que $P_2$ toca en al menos un punto a todos los lazos, exceptuando a $L_{2}$. A $L_{1}$ y $L_{5}$, los toca en el nodo $a$; a $L_{3}$ y $L_{4}$, los toca en, al menos, el nodo $f$.
$$\Delta_{3}=1-(L_{2}+L_{3}+L_{4})$$
En este caso, $P_3$ toca a $L_{1}$ y a $L_{5}$ en los nodos $a$, $b$ y $c$.
$$\Delta_{4}=1$$
$P_{4}$ toca a todos los lazos.
Una vez que se han definido todos los elementos del diagrama de flujo de señal, sólo queda sustituir en la fórmula de Mason, tal que:
$$FT=\frac{F(s)}{F(i)}=\frac{\sum_{k=1}^{N} P_k \Delta_k}{\Delta}$$
$${\scriptsize FT=\frac{P_{1}\Delta_{1}+P_{2}\Delta_{2}+P_{3}\Delta_{3}+P_{4}\Delta_{4}+P_{5}\Delta_{5}}{1-(L_{1}+L_{2}+L_{3}+L_{4}+L_{5})+(L_{1}L_{2}+L_{1}L_{3}+L_{1}L_{4}+L_{2}L_{4}+L_{5}L_{2}+L_{5}L_{3}+L_{5}L_{4})-(L_{1}L_{2}L_{4}+L_{5}L_{2}L_{4})}}$$
Para observar la función de transferencia desglosada, sólo es necesario sustituir los valores de los caminos directos, los lazos y los deltas en la expresión anterior.
De esta forma, se utiliza la fórmula de Mason para obtener la FT de sistemas complejos.

