Lugar geométrico de la raíz (LGR)

Este método nos sirve para identificar la estabilidad de un sistema de forma gráfica, además nos muestra que sucede con las variaciones de $K$ y para qué puntos el sistema es estable o inestable.

Para construir un LGR debemos de considerar las siguientes reglas:

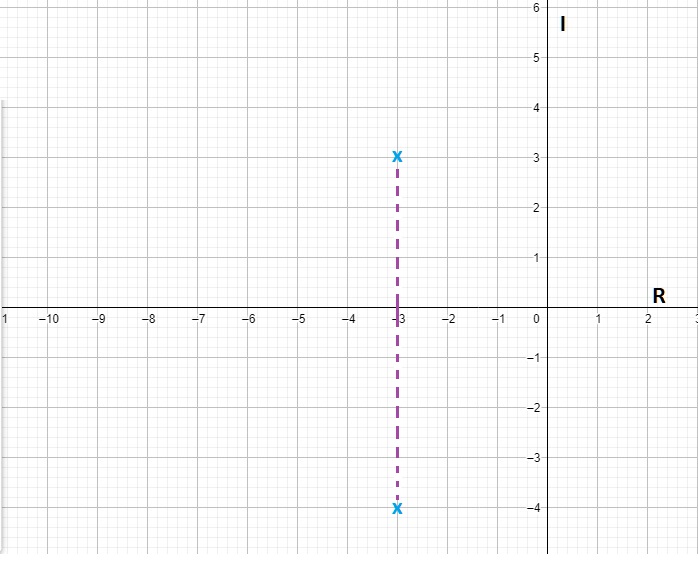
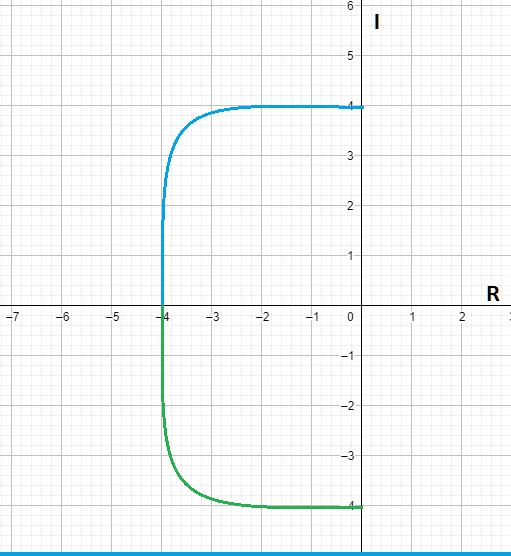
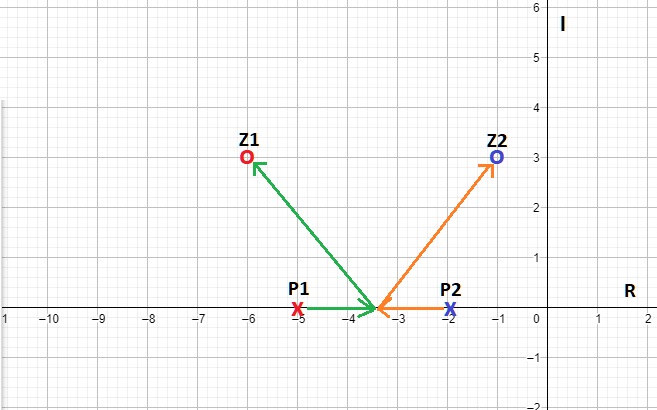
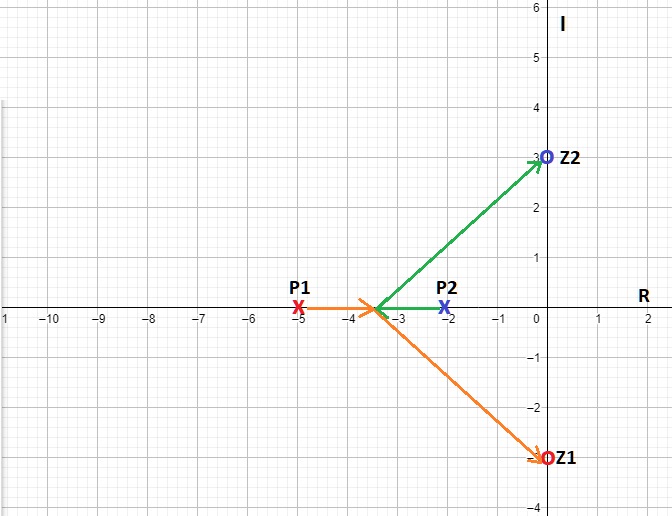
• Siempre debe de ser simétrico con respecto al eje real ${R}$, tal como se ve en la figura 1.

a)

b)

Fig.1. Simetría con respecto al eje de los reales $R$, en las figuras a) y b) se puede visualizar dicha simetría.

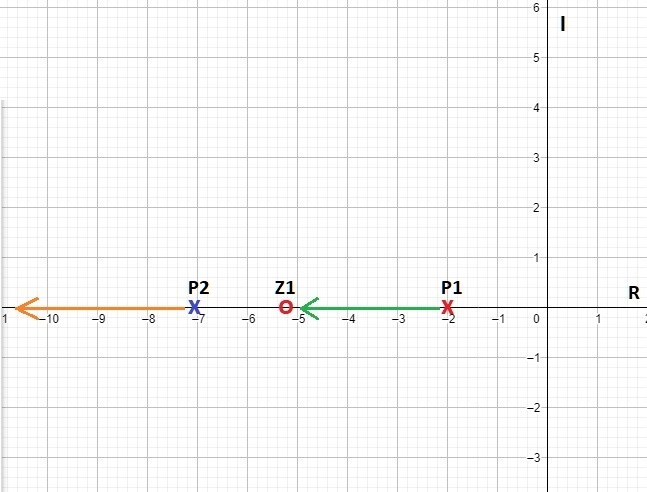
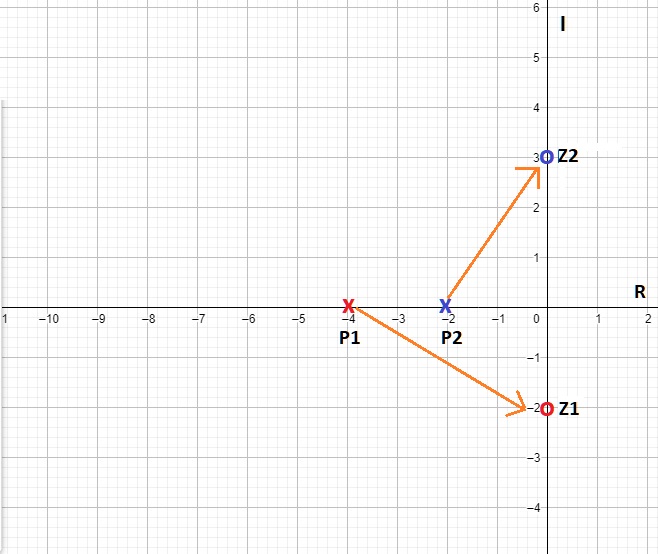
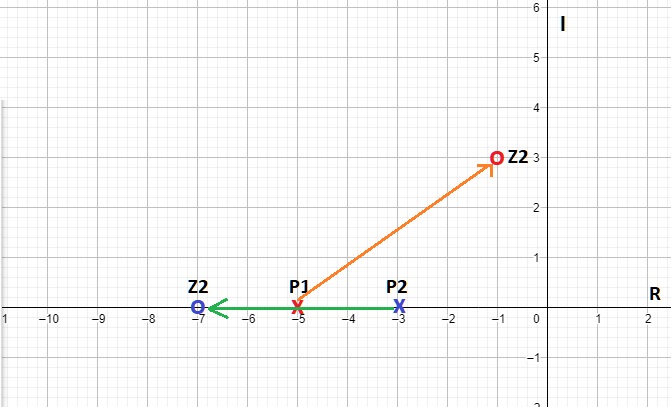
• Todos los polos ($P$) tienden a un cero ($Z$), es decir, siempre un polo va a buscar apuntar hacía un cero, ya sea que apunten a un $Z$ en el campo finito o a uno en el infinito, por ejemplo, si se tiene el sistema mostrado en la figura 2, es posible ver que el polo $P_1$ apunta hacía el cero  finito $Z_1$, mientras que el polo $P_2$ apunta a un cero en el infinito. A partir de aquí, gráficamente un polo está representado por una cruz, y un cero por un circulo.

Fig. 2. Se puede ver que el polo $P_1$ apunta hacía el cero  finito $Z_1$, mientras que el polo $P_2$ apunta a un cero en el infinito

• Siempre se debe de cumplir la condición de que $\#Z\leq \#P$, es decir, siempre deben de existir más o igual número de polos que de ceros. Si esta condición no se cumple, no se puede realizar el LGR.

Ahora bien, en este momento se debe de visualizar como construir el LGR. Para esto tenemos la siguiente metodología:

1. Calcular asíntotas, tal que:

$$\theta_{n}=\frac{(2k+1)180°}{\#P-\#Z}$$

Para $k=0, 1, \ldots,[(\#P-\#Z)-1]$

2. Calcular el punto del que parten las asíntotas:

$$\gamma=\frac{\sum polos -\sum ceros}{\#P-\#Z}$$

Donde $\sum polos$ es la sumatoria de los valores de todos los polos y $\sum ceros$ es la sumatoria de los valores de todos los ceros.

3. Nunca, pero nunca, se deben de cruzar las asíntotas, se pueden encontrar pero nunca pueden pasar sobre otras. Esta característica provoca que el cero hacía el que apunta un polo no sea definido, sino más que por el hecho de buscar asíntotas que no se crucen, esto quedará claro más adelante.

En la figura 3, se muestran algunos ejemplos de construcción del LGR incorrectos, así como uno correcto.

a)

b)

c)

d)

Fig. 3.-Dierentes ejemplos de construcciones del LGR. a) No es correcta ya que no hay ningún tipo de simetría. b) No es correcta ya que no hay simetría con respecto a $R$. c) Es correcta debido a que si existe simetría con respecto a $R$. d) No es correcta ya que no es simétrica y las asíntotas se están cruzando.

Ahora bien, se tiene el siguiente sistema, del cual hay que construir su LGR:

$$G(S)=\frac{1}{S-3}$$

Tal que $k={0}$.

Calculando:

$$\gamma=\frac{\sum polos -\sum ceros}{\#P-\#Z}=\frac{(0+3)-(0+0)}{1-0}=3$$

$$\theta_{1}=\frac{(2k+1)180°}{\#P-\#Z}=\frac{(2*0+1)180°}{1}=180°$$

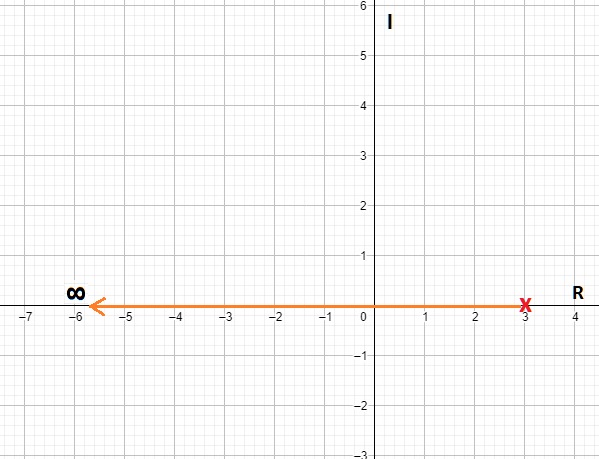
Lo que nos da como resultado el  gráfico de la figura 4:

Fig. 4. Como es posible ver, la asíntota parte del valor 3, es decir del mismo punto que el polo, y esta va con una dirección de 180° hacía un cero que se encuentra en el infinito, ya que la función no tiene ceros. Una importante nota es que un posible número $K$ (mayúscula) puede recorrer la asíntota (línea anaranjada) para definir los valores en los que el sistema será estable.

Ahora bien, si al sistema anterior agregamos el valor $K$ mayúscula tal que obtengamos el sistema de la figura 5, es posible notar que para que el sistema sea estable, se necesita un $K>3$.

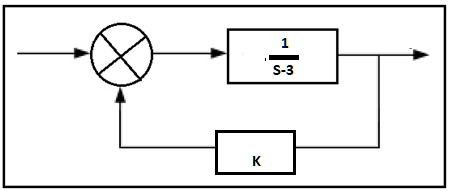
Fig. 5. Sistema con un valor $K$, el sistema se hace estable para un valor $K>3$.

Vamos a suponer ahora el siguiente sistema:

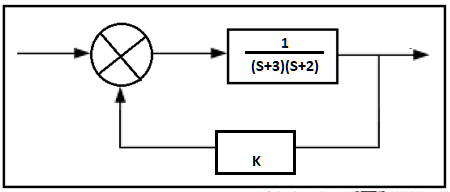
Tal que puede ser representado por

$$G(S)=\frac{1}{S^{2}+5S+6+K}$$

Calculamos las características del gráfico:

$$\gamma=\frac{\sum polos -\sum ceros}{\#P-\#Z}=\frac{(-3-2)-(0)}{2}=-2.5$$

$$\theta_{1}=\frac{(2k+1)180°}{\#P-\#Z}=\frac{(2*0+1)180°}{2}=90°$$

$$\theta_{2}=\frac{[(2*1)+1]180°}{2}=270°$$

Dando como resultado el gráfico de la figura 6.

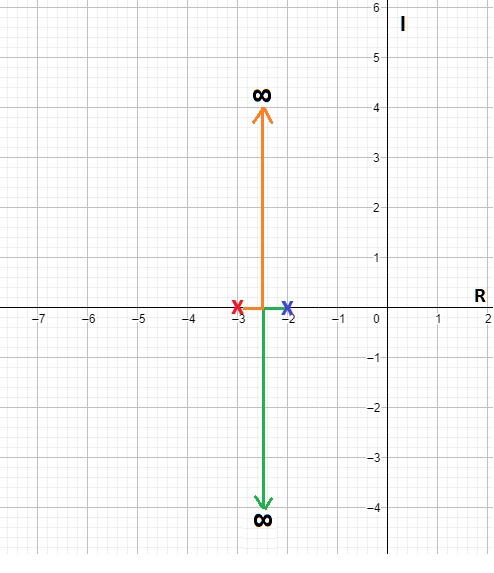Fig. 6. Podemos observar que las asíntotas inician en 2.5. Las asíntotas que salen de ambos polos se dirigen hacía el valor de $\gamma$ y en ese momento cambian su dirección hacía ceros en el infinito con 90 y 270 grados respectivamente.

Ahora, se el siguiente ejemplo:

$$G(S)=\frac{K}{(S+a)(S+b)(S+c)}$$

Calculamos los elementos del gráfico

$$\gamma=\frac{(-a-b-c)-(0)}{3-0}=\frac{-a-b-c}{3}$$

Tenemos que $k=\{0,1,2\}$, por lo que calculamos

$$\theta_{1}=\frac{(2*0+1)180°}{3}=60°$$

$$\theta_{2}=\frac{[(2*1)+1]180°}{3}=180°$$

$$\theta_{2}=\frac{[(2*2)+1]180°}{3}=300°$$

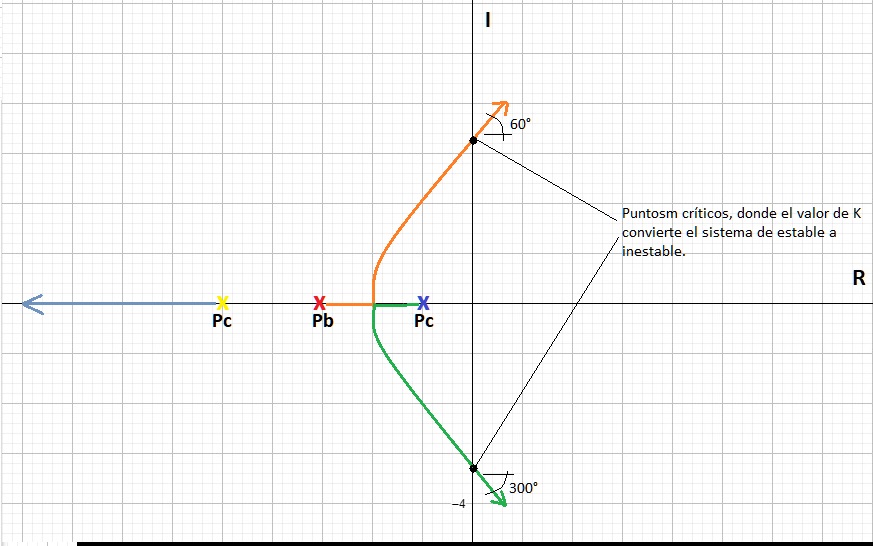
Con lo cual obtenemos la gráfica mostrada en la figura 7.

Fig. 7. En este gráfico se puede apreciar que los dos polos $P_b$ y $P_c$ inician su recorrido apuntando hacía el valor de $\gamma$ , en ese momento, la asíntota que sale del $P_b$ hace un cambio de dirección a un a razón de $\theta_{1}=60°$ , y la asíntota que sale de $P_a$, se mueve en dirección $\theta_{3}=300°$, mientras que $P_c$ busca un cero en el infinito con dirección de 180°.

Es importante mencionar en la figura 7, que las direcciones pueden modificarse, es decir $P_b$ puede apuntar hacia $\theta_{3}=300°$ y $P_a$ puede apuntar hacía $\theta_{1}=60°$, esto es indiferente, solo escogen la dirección para cumplir con la condición de que las asíntotas no se deben de tocar, se pueden encontrar pero nunca cruzarse.

Ahora, verifiquemos el comportamiento del siguiente sistema:

$$G(S)=\frac{K}{(S+a)(S+b)(S+c)(S+d)}$$

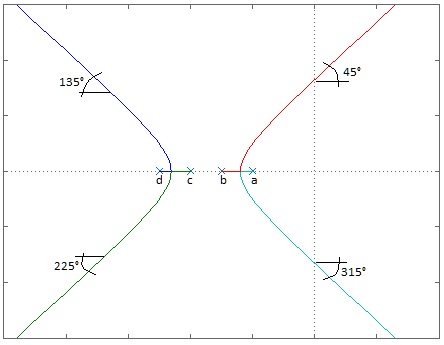
Tal que $\theta_{1}=45°$, $\theta_{2}=135°$, $\theta_{3}=225°$, $\theta_{4}=315°$

Con lo cual formamos la  figura 8:

Fig. 8. Se puede observar como cada uno de las asíntotas se dirige hacía un $\gamma$, cuando llegan a tal punto todas ellas se redirigen hacía una dirección en particular: $a\rightarrow 45°$, $b\rightarrow 315°$, $c\rightarrow 225°$ y $d\rightarrow 135°$. Obviamente cada una de las asíntotas, toma su dirección para evitar interponerse o cruzarse con cualquier otra.

Obviamente, de todos los ejemplos anteriores, es posible realizar el recorrido de $K$ sobre las asíntotas, y de esta forma determinar para que valores de $K$ el sistemas es estable e inestable,recordando que del lado izquierdo del plano es estable y del lado derecho es inestable.

LGR en Matlab

En las siguientes imágenes, se puede observar la construcción del LGR en Matlab (así como su función generadora), es posible notare que se respetan los hechos de que no se pueden tocar y de que debe de ser simétrico, también respetan la nomenclatura cruz para los polos y circulo para los ceros.

Con el código de Matlab:

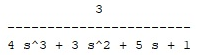
Y el gráfico del LGR que se puede fer en la figura 9:

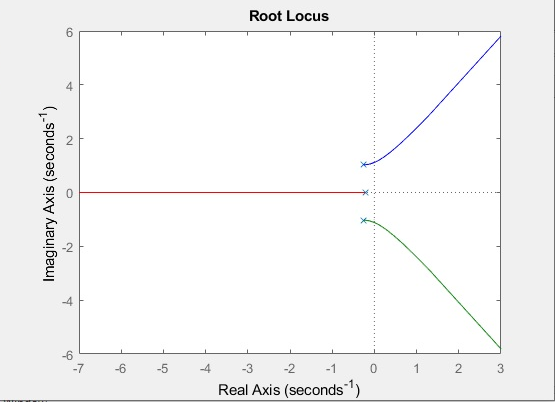
Fig. 9.- LGR obtenido por medio de Matlab.

Para el código:

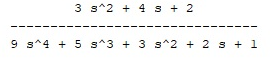
Obteniendo el gráfico de la figura  10.

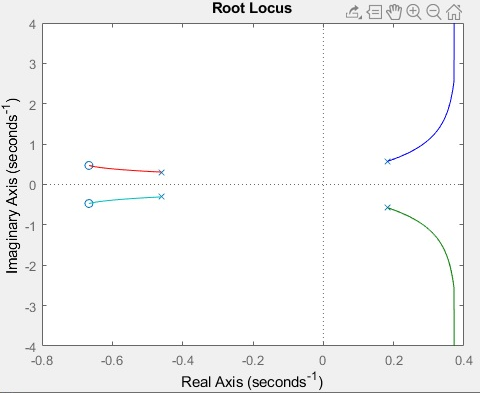
Fig. 10.- LGR obtenido por medio de Matlab.

Para el código:

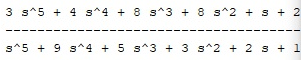
Y obtenemos:

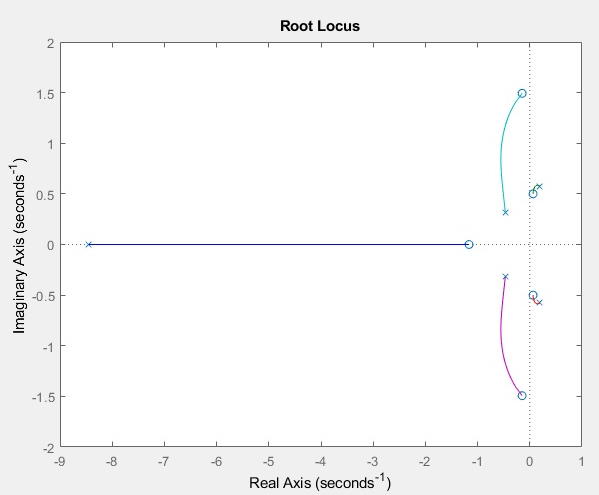
Fig. 10.- LGR obtenido por medio de Matlab.