Estabilidad
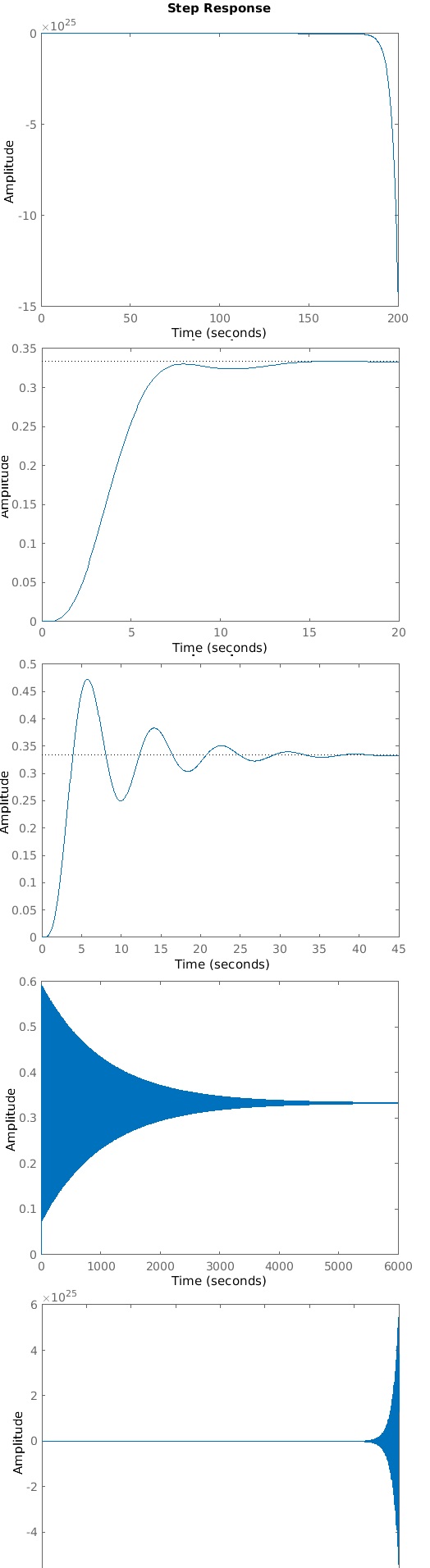
La estabilidad en un sistemas nos muestra si este va a comportarse de una forma adecuada, o si por el contrario el sistema terminara realizando acciones fuera de control o indebidas. Un sistema es estable si responde en forma limitada a una excitación limitada. También puede decirse que un sistema estable es aquel en que los transitorios decaen, es decir, la respuesta transitoria desaparece para valores crecientes del tiempo. La figura 1 muestra ejemplos de respuesta en el tiempo de sistemas inestables, y la figura 2 muestra ejemplos de respuesta de un sistema estable
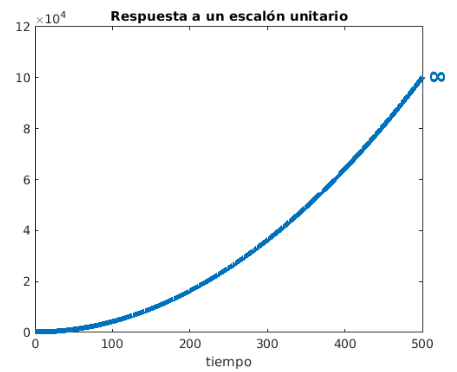
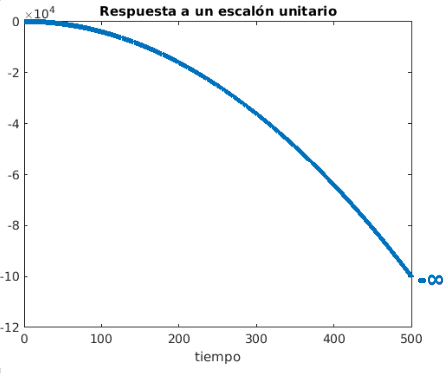
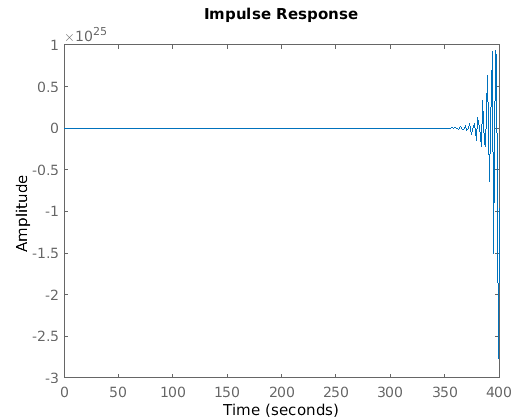
Fig. 1.- Ejemplos de respuesta en el tiempo de sistemas inestables, como se puede observar la inestabilidad implica un crecimiento hacía el infinito conforme el tiempo también tiende al infinito.
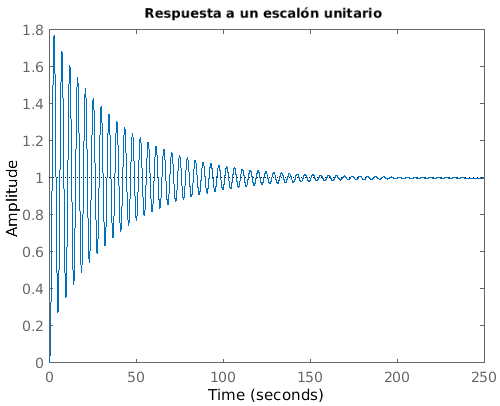
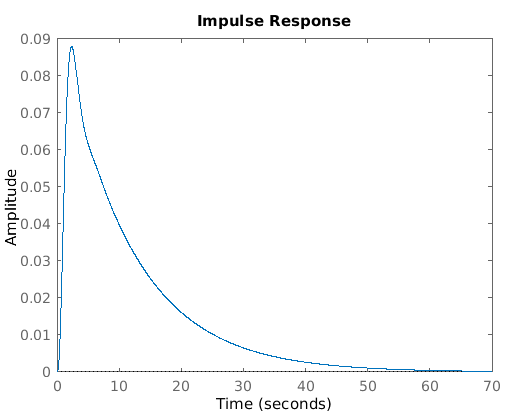
Fig. 2.- Ejemplos de respuesta en el tiempo de sistemas estables. Como es posible observar las gráficas presentan un comportamiento que tiende hacia un estado estacionario, y tiende a la eliminación de los transitorios.
La estabilidad está directamente ligada a los valores de los polos dentro de la ecuación que representa la función de transferencia de un sistema. El plano cartesiano mostrado en la figura 3, muestra precisamente las regiones en las cuales un sistema es estable o inestable, es decir, si uno de los polos del sistema se posiciona en la parte derecha de la gráfica, o en tiempo positivo, el sistema será inestable. Todos los polos deben de centrarse en el lado izquierdo del plano cartesiano para que el sistema sea estable.
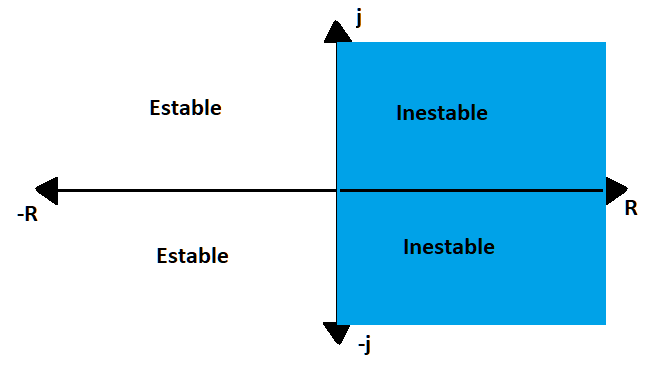
Fig. 3.- Representación del plano cartesiano donde se pueden observar las regiones donde los polos del sistema generan estabilidad o inestabilidad.
Por ejemplo, tenemos la siguiente función de trasferencia:
$$G(s)=\frac{(s+3)}{(s+1)(s+2)(s+4)}$$
Si graficamos los polos del sistema, vemos que todos se encuentran del lado izquierdo del plano, por lo que indicaría que el sistema es estable, como se ve en la figura 4.
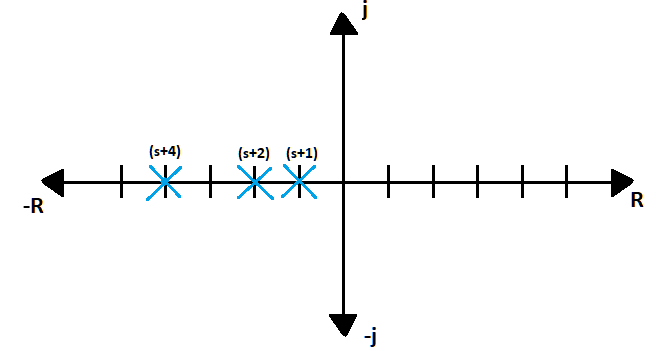
Fig. 4. Sistema con polos de lado izquierdo de la gráfica.
Sin embargo, si graficamos los polos del siguiente sistema:
$$G(s)=\frac{(s+3)}{(s+1)(s+2)(s+4)(s-5)}$$
Vemos que el polo $s=5$, se encuentra del lado derecho del plano, por lo que este polo genera la inestabilidad del sistema, como se ve en la figura 5. Basta con un solo polo en tal región para que el sistema sea inestable.
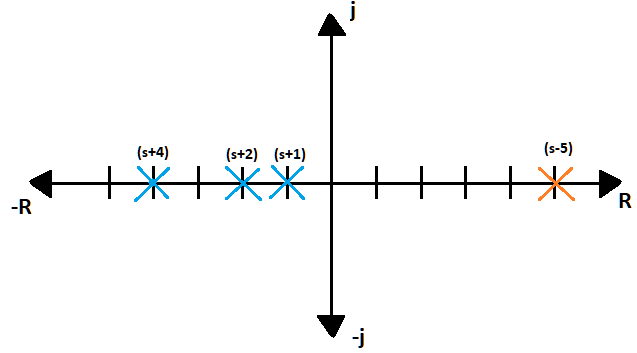
Fig. 5.- Sistema con un polo del lado derecho del plano, sistema inestable.
Ahora bien, vamos a suponer un sistema en la forma mostrada en la figura 6.
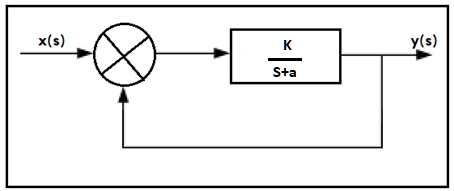
Fig. 6.- Sistema con un valor $K$ que puede moverse a través de la curva de estabilidad.
Podemos ver que el sistema de la figura 6 presenta una variable $K$, la cual puede generar un rango de valores dentro de la función de transferencia. Este valor $K$ puede adquirir valores que hagan estable el sistema, o valores que lo hagan inestable.
Bajo este esquema, si un sistema es inestable, podemos modificar el valor de $K$ para convertir a ese sistema en un modo estable. Por ejemplo, tenemos el sistema siguiente:
$$G(s)=\frac{1}{s-3+K}$$
Para este sistema podemos ver que el valor de determinará el comportamiento del mismo, puede adquirir los valores desde 0 hasta $\infty$. Evaluando valores para $K$ de 0 hasta 4 en el sistema anterior, tenemos:

Podemos ver que bajo este caso, el sistema se vuelve estable para $K\geq4$ , y para $K<4$ el sistema es inestable.
Para identificar la inestabilidad de un sistema, tenemos diferentes métodos, entre ellos se encuentra el método de Ruth-Hurwitz, que nos permite identificar si un sistema es estable o no, sin la necesidad de factorizar el polinomio característico (el polinomio que está en el denominador de la función de transferencia), ahora bien, si tenemos el siguiente polinomio característico:
$$a_{0}S^{n}+a_{1}S^{n-1}+\cdots+a_{n-1}S^{1}+a_{n}=0$$
Ordenamos los coeficientes en $n+1$ filas, como podemos observar en la siguiente representación ordenada, la fila $s^{n}$ tiene todos los coeficientes de las posiciones pares del polinomio, mientras que la fila $s^{n-1}$ tiene todos los coeficientes de las posiciones impares del polinomio. A partir de estas dos primeras filas del conjunto ordenado, se van a ir construyendo las filas adicionales, la cantidad de filas dependerá del sistema.
\begin{matrix}
s^{n} & a_0 & a_2 & a_4 & a_6 & \cdots \\
s^{n-1} & a_1 & a_3 & a_5 & a_7 & \cdots \\
s^{n-2} & b_1 & b_2 & b_3 & b_4 & \cdots \\
s^{n-3} & c_1 & c_2 & c_3 & c_4 & \cdots \\
s^{n-4} & d_1 & d_2 & d_3 & d_4 & \cdots \\
\vdots & \vdots & \vdots & & & \\
s^{2}& e_1 & e_2 & & & \\
s^{1}& f_1 & & & & \\
s^{0}& g_1 & & & & \\
\end{matrix}
Para determinar la estabilidad de nuestro sistema, es necesario calcular los valores $b_{n}, c_{m}, d_{i}, \ldots,g_{1}$ , para formar las filas $s^{n-2}, s^{n-3}, \ldots,s^{0}$. Para calcular estos valores nos vamos a basar en las siguientes expresiones:
$$\begin{matrix}
b_{1}=\frac{a_{1}a_{2}-a_{0}a_{3}}{a_1} & b_{2}=\frac{a_{1}a_{4}-a_{0}a_{5}}{a_1} & b_{3}=\frac{a_{1}a_{6}-a_{0}a_{7}}{a_1} & \cdots \\
c_{1}=\frac{b_{1}a_{3}-a_{1}b_{2}}{b_1} & c_{2}=\frac{b_{1}a_{5}-a_{1}b_{3}}{b_1} & c_{3}=\frac{b_{1}a_{7}-a_{1}b_{4}}{b_1} & \cdots\\
d_{1}=\frac{c_{1}b_{2}-b_{1}c_{2}}{c_1}& d_{2}=\frac{c_{1}b_{3}-b_{1}c_{3}}{c_1} & & \cdots \\
\vdots & \vdots & &
\end{matrix}$$
Estas evaluaciones se llevan a cabo hasta que ya no se tienen valores numéricos en las columnas más que cero.
Este criterio dice que un sistema es estable, si todos los elementos que se encuentran en la primera columna de la estructura ordenada tienen el mismo signo siempre, si existe un cambio de signo en tal columna, el sistema es inestable.
Para entender un poco mejor, vamos a realizar el siguiente ejemplo:
Tenemos el siguiente polinomio característico:
$$5s^{4}+6s^{3}+7s^{2}+8s^{1}+9=0$$
Observamos que en tal polinomio $a_{0}=5$, $a_{1}=6$, $a_{2}=7$, $a_{3}=8$ y $a_{4}=9$.
Iniciamos ordenando los coeficientes en la siguiente forma
$$\begin{matrix}
s^{4} & 5 & 7 & 9\\
s^{3} & 6 & 8 & 0\\
s^{2} & & & \\
s^{1} & & & \\
s^{0} & & &
\end{matrix}$$
Aquí es importante notar que en la primera fila que son las posiciones pares, se colocan los coeficientes de tales posiciones, solo que para fines explicativos y demostrativos, dichos coeficientes son impares (los coeficientes son los impares, no la posición de ellos). Lo mismo pasa con la segunda fila, en donde van los coeficientes de las posiciones impares del polinomio, las posiciones son las impares, aunque los valores de tales coeficientes son impares.
Calculamos:
$$b_{1}=\frac{(6)(7)-(5)(8)}{6}=\frac{1}{3}$$
$$b_{2}=\frac{(6)(9)-(5)(0)}{6}=9$$
Al ya no haber columna para poder calcular un posible valor $b_{3} $, damos por concluido el cálculo de la fila , quedando
$$\begin{matrix}
s^{4} & 5 & 7 & 9\\
s^{3} & 6 & 8 & 0\\
s^{2} & \frac{1}{3} & 9 & \\
s^{1} & & & \\
s^{0} & & &
\end{matrix}$$
Ahora, se procede a calcular los valores de la fila $s^{3}$, para lo cual utilizamos las mismas expresiones, es importante notar que el proceso es completamente metódico, y aprendiendo a realizarlo una vez, es posible realizarlo sin ningún problema para más ejemplos.
$$c_{1}=\frac{(\frac{1}{3})(8)-(9)(6)}{\frac{1}{3}}=-154$$
Al ya no haber más columnas para poder realizar el cálculo de un posible $c_{2}$ , asumimos que hemos concluido con esta fila. Cuando se ha obtenido una fila con un solo coeficiente, como en este caso solo $c_{1}$, debajo de tal valor colocamos el coeficiente independiente, en este caso el valor 9, dándonos como resultado:
$$\begin{matrix}s^{4} & 5 & 7 & 9\\
s^{3} & 6 & 8 & 0\\ s^{2} & \frac{1}{3} & 9 & \\ s^{1} &-154 & & \\ s^{0} & 9 & & \end{matrix}$$
Como podemos observar, el sistema es inestable, ya que en la primera columna hay un cambio de signo de $\frac{1}{3}$ a $-154$ y un cambio de signo de $-154$ a $9$.
Ahora, vamos a suponer un polinomio característico con la forma:
$$3s^{5}+5s^{4}+7s^{3}+9s^{2}+6s^{1}+4=0$$
Realizando el ordenamiento de los datos tenemos
$$\begin{matrix}
s^{5} & 3 & 7 & 6\\
s^{4} & 5 & 9 & 4\\
s^{3} & & & \\
s^{2} & & & \\
s^{1} & & & \\
s^{0} & & &\\
\end{matrix}$$
De la misma forma que en el caso anterior, iniciamos los cálculos para llenar la tabla ordenada de coeficientes:
$$b_{1}=\frac{(5)(7)-(9)(3)}{5}=\frac{8}{5}=1.6$$
$$b_{2}=\frac{(5)(6)-(4)(3)}{5}=\frac{18}{5}=3.6$$
Lo que nos da:
$$\begin{matrix}
s^{5} & 3 & 7 & 6\\
s^{4} & 5 & 9 & 4\\
s^{3} & 1.6 & 3.6 & \\
s^{2} & & & \\
s^{1} & & & \\
s^{0} & & &\\
\end{matrix}$$
Continuando con la siguiente fila:
$$c_{1}=\frac{(1.6)(9)-(3.6)(5)}{1.6}=\frac{-3.6}{1.6}=-2.25$$
$$c_{2}=\frac{(1.6)(4)-(0)(5)}{1.6}=\frac{6.4}{1.6}=4$$
Dando como resultado:
$$\begin{matrix}
s^{5} & 3 & 7 & 6\\
s^{4} & 5 & 9 & 4\\
s^{3} & 1.6 & 3.6 & \\
s^{2} &-2.25 &4 & \\
s^{1} & & & \\
s^{0} & & &\\
\end{matrix}$$
Para la siguiente fila tenemos:
$$c_{2}=\frac{(-2.25)(3.6)-(4)(1.6)}{-2.25}=\frac{-14.5}{-2.25}=6.44$$
Como ya no podemos calcular más coeficientes, y como solo calculamos un coeficiente, ahora debajo de él va el coeficiente independiente del polinomio, de tal forma que
$$\begin{matrix}
s^{5} & 3 & 7 & 6\\
s^{4} & 5 & 9 & 4\\
s^{3} & 1.6 & 3.6 & \\
s^{2} &-2.25 &4 & \\
s^{1} & 6.44 & & \\
s^{0} & 4 & &\\
\end{matrix}$$
Nuevamente, es posible ver que se trata de un sistema inestable, debido a que hay cambios de signos en la primera columna, entre +1.6 y -2.25; y -2.25 y +6.44.
Ahora, si tenemos un polinomio en la siguiente forma:
$$3s^{4}+9s^{3}+9s^{2}+6s^{1}+3K=0$$
Como podemos observar, este polinomio tiene una variable $K$, esta variable es muy importante, ya que ella es la que definirá si este sistema es estable o inestable, y también definirá los valores para los cuales se cumple la estabilidad, el proceso del cálculo es exactamente igual que en los ejemplos anteriores, solo que en este caso vamos a ir arrastrando simbólicamente la variable $K$. Acomodamos los coeficientes según la tabla:
$$\begin{matrix}
s^{4} & 3 & 9 & 3K\\
s^{3} & 9 & 6 & 0 \\
s^{2} & & & \\
s^{1} & & & \\
s^{0} & & &\\
\end{matrix}$$
Calculamos la primera fila de coeficientes:
$$b_{1}=\frac{(9)(9)-(6)(3)}{9}=\frac{63}{9}=7$$
$$b_{1}=\frac{(9)(3K)-(0)(3)}{9}=\frac{27K}{9}=3K$$
Dando como resultado:
$$\begin{matrix}
s^{4} & 3 & 9 & 3K\\
s^{3} & 9 & 6 & 0 \\
s^{2} & 7 & 3K & \\
s^{1} & & & \\
s^{0} & & &\\
\end{matrix}$$
Continuando con la siguiente fila:
$$c_{1}=\frac{(7)(6)-(3K)(9)}{7}=\frac{42-27K}{7}=\frac{42}{7}-\frac{27K}{7}=6-3.85K$$
Como ya no se pueden calcular más elementos de la fila y solo se calculó un solo coeficiente, colocamos debajo de él, el valor del coeficiente independiente, quedando:
$$\begin{matrix}
s^{4} & 3 & 9 & 3K\\
s^{3} & 9 & 6 & 0 \\
s^{2} & 7 & 3K & \\
s^{1} & 6-3.85K & & \\
s^{0} & 3K & &\\
\end{matrix}$$
Ahora, ¿Cómo se hace ese sistema estable?. la respuesta es simple, es posible ver que los primeros tres elementos de la columna principal son positivos, por lo tanto los últimos dos elementos también deben de ser positivos, es decir,
$$6-3.85K>0$$
$$3K>0$$
Podemos definir fácilmente el rango de valores de $K$ del último elemento de la columna, simplemente , para que el último valor de la columna de siempre un valor positivo.
Para que el penúltimo valor de la columna de siempre positivo, necesitamos encontrar el rango de valores para los que $K$ da positivo, tal que:
\begin{matrix}
6-3.85K>0\\
-3.85K>-6\\
3.85K<6\\
K<\frac{6}{3.85}
\end{matrix}
Por lo que vemos que $K$ debe ser menor que $\frac{6}{3.85} = 1.558$ (este límite lo pone el penúltimo elemento de la columna), y mayor que 0 (este límite lo pone el último elemento de la columna), tal que
$$0<K<\frac{6}{3.85}$$
Y de esta forma encontramos el rango de valores de $K$ para los que el sistema es estable.
Para poder simular el criterio de Ruth-Hurwitz en Matlab, se puede descargar el siguiente código:
El proyecto original puede ser descargado y visualizado desde:
https://la.mathworks.com/matlabcentral/fileexchange/17483-routh-hurwitz-stability-criterion
Verificación en Matlab
Vamos a verificar el último de los ejercicios realizados, y ver como se comporta este sistema con diferentes valores de Matlab, para esto vamos a utilizar valores de $K=\{-1, .5, 1, 1.55. 1.56\}$. Recordando que para que el sistema sea estable se debe de cumplir $0<K<\frac{6}{3.85}$.
Vamos a utilizar el siguiente código de Matlab:
|
1 2 3 4 5 |
K=1.56; num=K; den=[3 9 9 6 3*K]; Salida=tf(num,den) step(Salida) |
En el código, se va a ir sustituyendo los valores mencionados de $K$, lo que nos dará las gráficas de la figura 7.