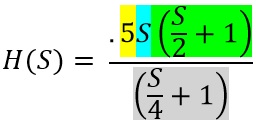Respuesta en frecuencia
En otra página de esta web (http://virtual.cuautitlan.unam.mx/intar/ime/sistemas-de-primer-orden/ ) se había visto como probar un sistema con las señales de entrada Escalón, Rampa y Pulso unitario. Sin embargo, existe una señal de prueba adicional, pero esta tiene un comportamiento completamente diferente dentro del sistema a las señales mencionadas, en este caso la señal de entrada con la que también se puede probar un sistema es por medio de una señal senoidal.
Se ingresa la señal senoidal al sistema, y puede suceder que la señal se atenúe o que la señal se desfase. Para poder calcular la atenuación y desfase que sufre una señal cuando se ingresa al sistema, utilizamos los diagramas de Bode, o la respuesta en frecuencia de un sistema. Esto quiere decir, que los sistemas cambian sus condiciones de funcionamiento de acuerdo a la frecuencia en la que se trabaje, es decir, cada sistema debe ser diseñado para un rango de frecuencias óptimas, si se salen de ese rango de frecuencias, los sistemas pueden generar mal funcionamiento e inestabilidad.
Para analizar este comportamiento, se utiliza una escala logarítmica, ya que permite visualizar una gran cantidad de frecuencias es un espacio muy reducido, por ejemplo podemos visualizar frecuencias que van de .1 HZ hasta 100 Khz en una sola hoja.
Ahora bien, suponemos que tenemos un sistema de la forma:
$$
\begin{equation}
H(S)=\frac{S(S+2)}{(S+4)}
\end{equation}
$$
Para poder realizar el análisis, necesitamos obtener polos y ceros con la forma $\frac{S}{N}+1$ , donde $N$ es un valor numérico. Por tal motivo, de la ecuación (1), factorizamos 2 en el cero y 4 en el polo, para este fin, multiplicamos $S$ en el polo y en el cero por un uno algebraico, definido como:
$$
\begin{equation}
H(S)=\frac{S\left(S\frac{2}{2}+2\right)}{\left(S\frac{4}{4}+4\right )}=\frac{2S\left(\frac{S}{2}+1\right)}{4\left(\frac{S}{4}+1\right )}
\end{equation}
$$
Como es posible ver, la multiplicación por el uno algebraico solo se realizó para poder factorizar 2 y 4 del cero y del polo respectivamente, para obtener sus representaciones en la forma $\frac{S}{N}+1$. A la ecuación (2), ahora se le convierte en una representación logarítmica en la forma:
$$20logH(S)=\frac{2S\left(\frac{S}{2}+1\right)}{4\left(\frac{S}{4}+1\right )}=\frac{.5S\left(\frac{S}{2}+1\right)}{\left(\frac{S}{4}+1\right )}$$
$$
\begin{equation}
20logH(S)=20log 0.5+20log S+20log \left(\frac{S}{2}+1\right)-20log \left(\frac{S}{4}+1\right )
\end{equation}
$$
En la ecuación 3, hay que darse cuenta que el 20 log se le aplica a cada uno de los componentes de la ecuación que forman la función. También hay que notar que los elementos del numerador están en positivo y los elementos del denominador, o polos, se encuentran como negativos.
Ya habiendo entendido esta parte, podemos realizar el primer ejercicio de respuesta en frecuencia. Para esto hay que visualizar las reglas que tenemos para formar los trazos de Bode, para los trazos de bode es necesario realizar dos gráficas, una correspondiente a la atenuación/amplificación, y la otra gráfica correspondiente al desfase que sufre la señal. Estas reglas las podemos ver en la siguiente tabla, observando que se tienen reglas para amplitud y fase:
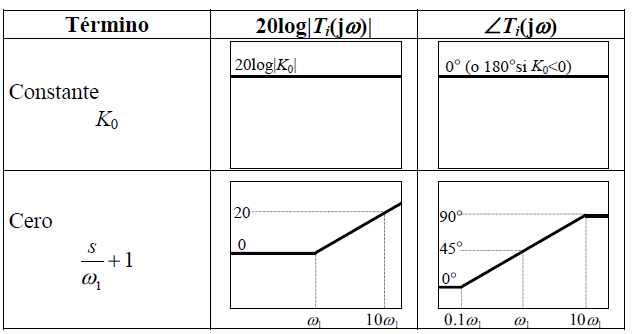
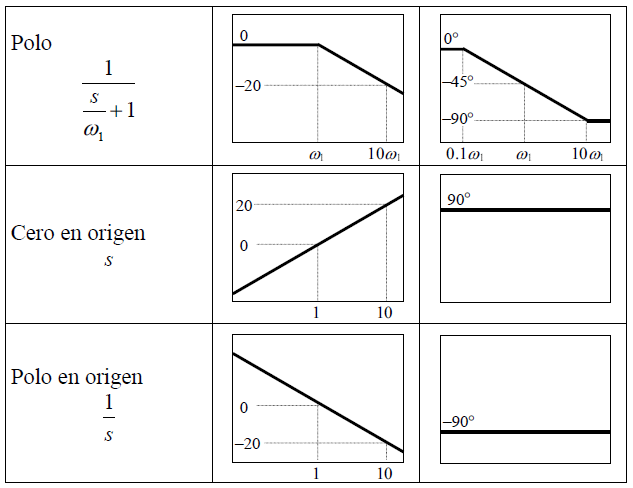
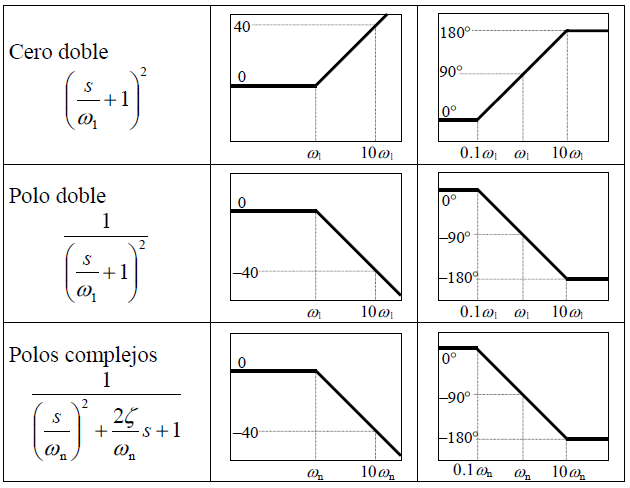
Tabla1.- Reglas para la construcción de los diagramas de bode, reglas en amplitud y desfase.
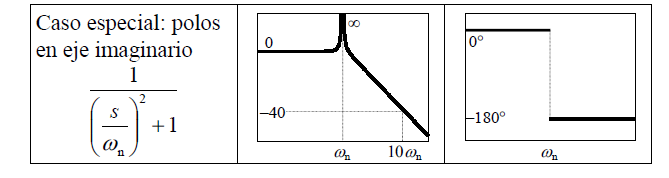
En la tabla 1 se puede observar que hay una regla para cada posible situación, polos y ceros en el origen, polos y ceros en un punto determinado $\omega_{n}$, así como polos y ceros complejos .
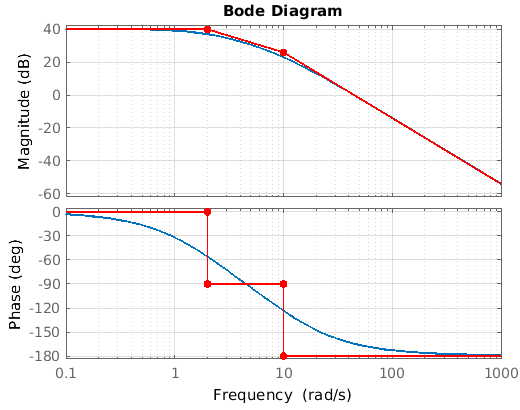
Remarcando que en el caso de la amplitud, podemos ver que si existe un polo en $\frac{S}{\omega_{1}+1}$ , la gráfica va a iniciar precisamente en $\omega_{1}$, y va a ir creciendo a razón de 20dB por década, lo que significa que en la siguiente década de la escala logarítmica, en $10\omega_{1}$, la línea habrá subido 20 decibles, está pendiente subirá hasta el infinito. En el caso del diagrama de fase vemos que tenemos que también representa a $\frac{S}{\omega_{1}+1}$ , sin embargo, en este caso vemos que inicia en $\frac{\omega_{1}}{10}$ y termina en $10\omega_{1}$, es decir, inicia una década antes y termina una década después de la posición señalada, aquí solamente sube o baja dos décadas, a raíz de 45° por década, estos comportamientos lo podemos percibir en la figura 2, donde se muestra en anaranjado la relación de incremento o decremento (según sea cero o polo, respectivamente), y se muestra en azul el inicio y termino de la pendiente.
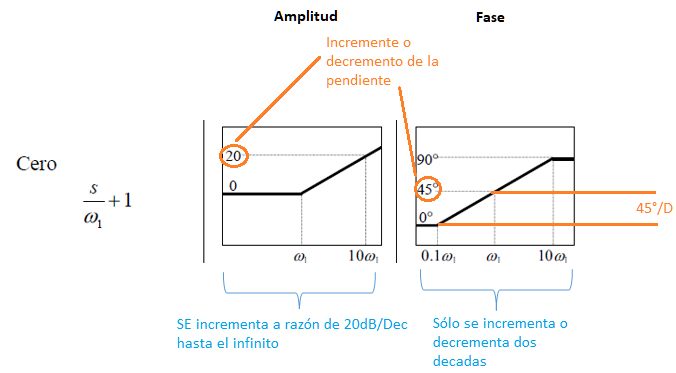
Fig. 2.- Ejemplo de inició y termino de las gráficas que pertenecen a cada polo o cero del sistema.
Esta interpretación se puede realizar en cada una de las reglas de la tabla, donde se ve el incremento, decremento, razón de incremento y tiempo de la pendiente, de cada uno de los posibles elementos que componen una función.
Ahora, bien ya explicada la interpretación y las bases para la realización del gráfico, procedemos a su realización.
Vamos a realizar el gráfico que representa a la función de transferencia:
$$20logH(S)=\frac{2S\left(\frac{S}{2}+1\right)}{4\left(\frac{S}{4}+1\right )}=\frac{.5S\left(\frac{S}{2}+1\right)}{\left(\frac{S}{4}+1\right )}$$
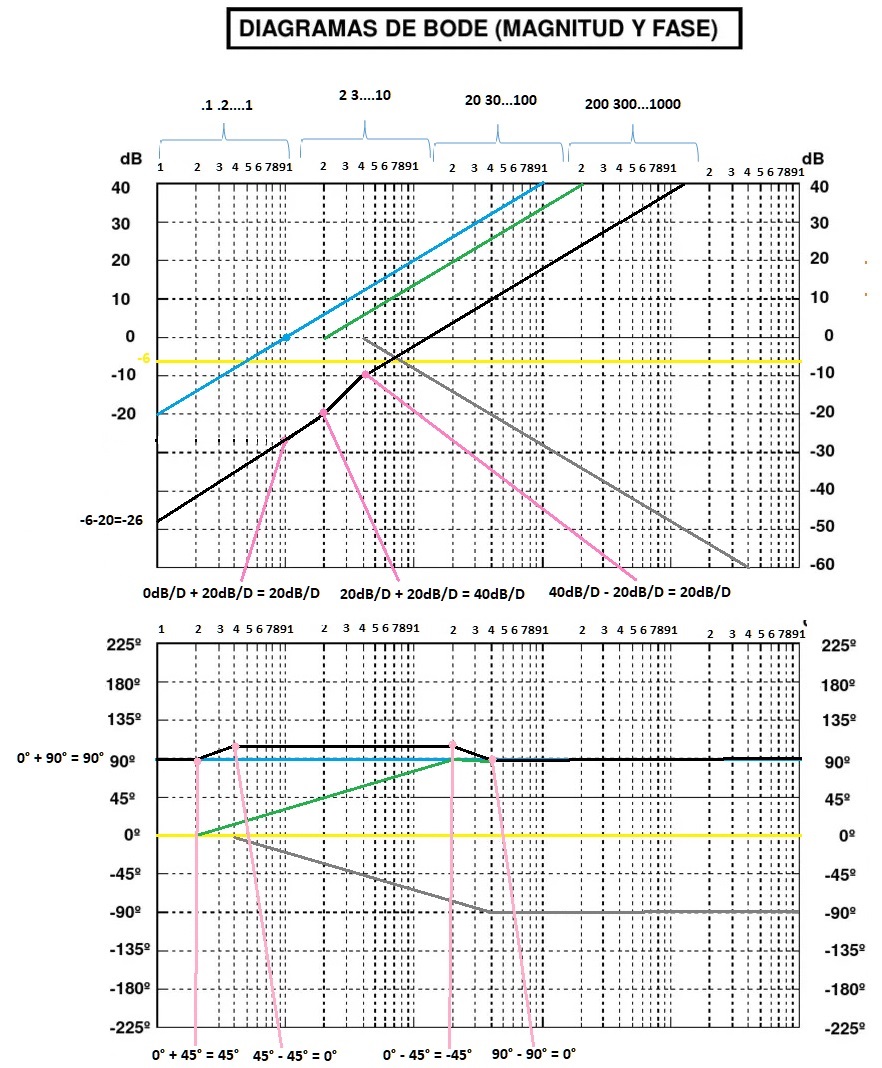
La función de transferencia nos da la figura 4, haciendo notar que en el eje de las Y, se encuentran los decibeles y grados (para magnitud y desfase, respectivamente), y en el eje de las X, se encuentran las frecuencias, que como se indica van desde .1 hasta 10000.
Para identificar cada uno de los trazos que corresponde a cada uno de los elementos de la función de transferencia, nos vamos a auxiliar de la figura 3, en donde se identifica cada elemento con un color determinado, color que posteriormente será utilizado en las gráficas de bode.
Fig. 3.- Representación en colores de la función de transferencia a graficar en el esquema de Bode.
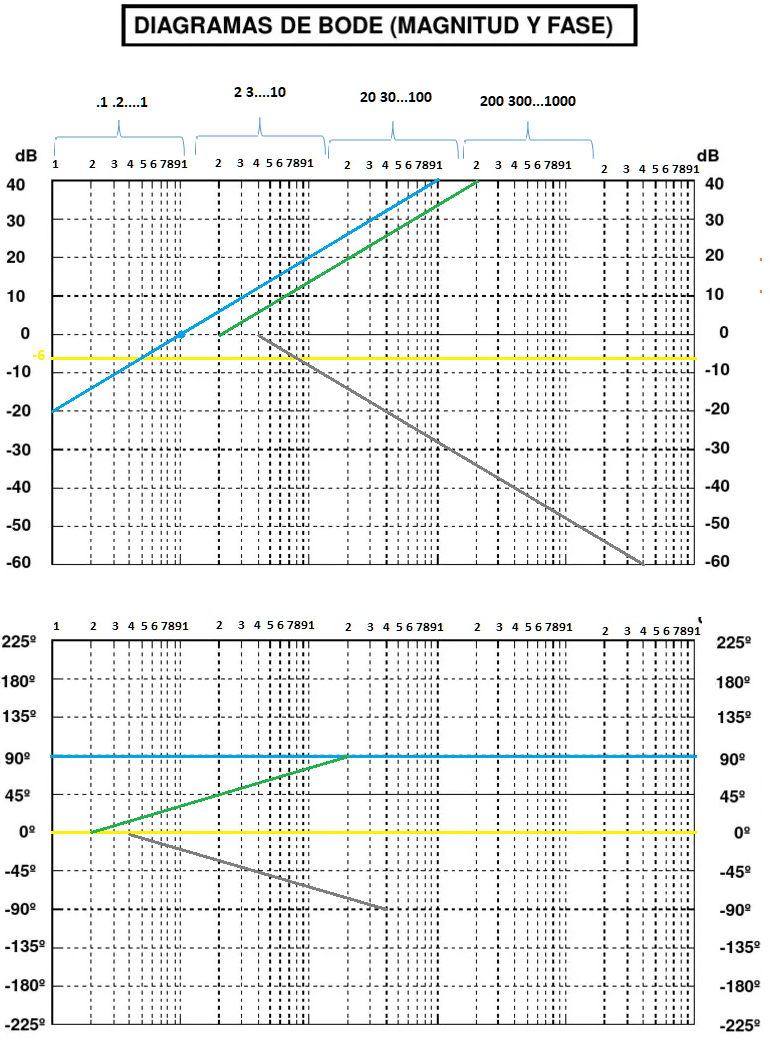
Fig. 4.- Diagramas de Bode, el diagrama superior representa la amplitud de la señal, el diagrama inferior representa el desfase de la señal. Sólo se han colocado los trazos que representan a cada uno de los elementos de la figura 3.
Analizando el diagrama de la magnitud en la figura 4, vemos que la primera parte de la función de transferencia es .5, por lo que $20log0.5=-6dB$, según la tabla de las propiedades para el trazado, cuando se trata de una constante, simplemente se traza una línea recta en el valor de la constante, esta línea la vemos en amarillo en $-6 dB$. La segunda parte de la función de transferencia es un cero en el origen es decir $S=0$, remarcada con azul en la función, según la tabla dice que cuando se tiene un cero en el origen, el trazo se inicia en $-20dB$, sube a razón de $20 dB/D$, y debe de cruzar por 1 (este punto se logra en la coordenada $(0 dB, 1)$ este cruce se marcó con un puntito azul. Ahora se tiene un cero que inicia en 2, y sube con una pendiente a razón de $20 dB/D$ hasta el infinito, lo cual se ve con eltrazo verde. Por último tenemos un polo que inicia en 4, pero como es polo inicia una pendiente descendiente a razón de $-20 dB/D$, que se ve como la línea gris.
En el caso de la fase, se puede ver de igual forma que para el primer elemento, según la tabla dice que si es una constante, se traza una línea recta en $0°$ (si la constante fuera menor que 0, la línea se traza en $180°$), por lo que se traza la línea amarilla. Para el segundo elemento, se tiene un cero en el origen, según la tabla, esto significa que se traza una línea recta en $90°$, indicada con la línea azul. Para el tercer elemento, se tiene un cero que marca el valor 2, sin embargo, según la tabla, la gráfica debe de iniciar en .2 subir a una razón de $45°$ por década y terminar en 20, comportamiento que se ve claramente en la línea verde. Por último, tenemos un polo que marca 4, según la tabla, iniciamos en .4, bajamos a una razón de $-45°/D$ hasta llegar a 40 (Es decir recorremos dos décadas), lo que se ve claramente con el trazo gris.
Ya habiendo explicado lo que significan cada uno de los trazos, es necesario decir, que este no es el resultado final, ya que el resultado final se definirá sumando todos y cada uno de los puntos que se involucran en las gráficas, estos puntos de suma los colocaremos en cada momento que una línea nazca o desaparezca en la forma mostrada en la figura 5:
Fig. 5.- Suma de los trazos independientes de cada elemento para obtener el comportamiento general del sistema, este comportamiento se puede ver en la línea gris de ambos diagramas.
El trazo negro de la figura 5, es el comportamiento del sistema con respecto a las frecuencias. Ahora bien, ¿Cómo se forman tales gráficas negras?. Estas se forman con la suma de los puntos de inicio y con las sumas de las pendientes, cada que inicia o termina una pendiente, nosotros realizamos una suma en dB o en ángulos, según sea la tabla a realizar.
Iniciamos con la fase, vemos que nuestra línea inicia en -26 dB, esto debido a que originalmente tenemos una línea amarilla que inicia en -6 dB y una línea azul que inicia en -20 dB, si sumamos esos dos puntos nos da como resultado -26 dB. Ya que definimos el punto de partida, vamos a ir sumando las pendientes en dB/D. Vemos que iniciamos la línea negra con un ascenso de 20 dB/D, ya que en ese momento sumamos la pendiente de la línea azul, está pendiente es de 20 dB/D, pero este crecimiento solo se da hasta el punto en que nace la línea verde, en ese momento, podemos ver que la pendiente verde va a razón de 20 dB/D, por lo que en ese punto existen dos ascensiones a razón de 20 dB/D, sumando ambas nos da una sección de la línea negra que asciende a razón de 40 dB/D. Esta ascensión de la línea negra a razón de 40 dB/D llega hasta el punto en donde nace la línea gris, vemos que la línea gris decrece a razón de -20 dB/D, por lo tanto 40 dB/D – 20 dB/D = 20 dB/D, la línea negra en este momento vuelve a ascender a razón de 20 dB/D, continuando este comportamiento hasta el infinito. En el gráfico se señaló cada uno de los puntos en donde cambia la pendiente con un punto rosa, señalando también la operación realizada en cada punto.
Ahora tenemos la gráfica de la fase, para esta de igual manera que la de magnitud, necesitamos definir el punto de inicio de la gráfica, para este caso tenemos una línea azul que está en 90°, y una línea amarilla que se encuentra a 0°, por lo tanto 90° + 0° = 90°, es el punto dónde inicia la línea negra, como no hay pendiente en ese punto, la línea continua con una razón de 0° hasta el punto donde nace la línea verde, la línea verde crece a razón de 45°/D, por lo que sumamos estos 45° a los 0° con los que estaba caminando la línea negra, en este momento la línea negra cambia a razón de 0° + 45° = 45°. Comienza a crecer a razón de 45°/D hasta donde nace la línea gris. En este punto se tiene una suma de 45° (negra)- 45° (gris) = 0°, en este momento, se puede ver la línea negra sigue hacía adelante pero con una razón de crecimiento de 0°, hasta llegar a punto donde la línea verde detiene su ascensión. En este momento tenemos una suma de 0° – 45° = -45°, que es la razón a la que cambio la línea negra, asciende a 45°/D, hasta llegar al punto donde la línea gris detiene su crecimiento. En este punto se suman todos los valores de los cambios de las líneas verde y gris, en este caso tenemos 90° de la línea verde, -90° de la línea gris, por lo que realizando la suma de esos cambios tenemos que 90° – 90° = 0°, que como podemos ver es la última relación de cambio de la línea negra. Al ya no haber más cambios más adelante, esta línea permanece a 0° hasta el infinito. En el gráfico se señaló cada uno de los puntos en donde cambia la pendiente con un punto rosa, señalando también la operación realizada en cada punto.
Bode en Matlab
Para obtener la gráfica de Bode en Matlab del ejemplo dado, sólo es necesario colocar el siguiente código:
|
1 2 3 |
funcion=tf([1 2 0], [1 4]); bode(funcion,{.1,1000}) grid |
Haciendo notar que los valores de la función de transferencia vienen de la ecuación:
\begin{equation}
H(S)=\frac{S(S+2)}{(S+4)}=\frac{(S^{2}+2S)}{(S+4)}
\end{equation}
$$
|
1 2 3 |
H = tf([100],[.05 .6 1]); bode(H) asymp(H) |
Que nos da como resultado:
Fig.7.- Resultado de la función asymp ( ), en azul tenemos la gráfica que Matlab por default nos arroja, y en verde se tienen las asíntotas con las cuales se forma la gráfica.
Referencias